Υδραυλικός ανυψωτήρας
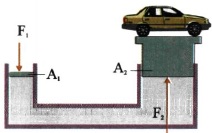
Στο παραπάνω σχήμα φαίνεται ένας υδραυλικός ανυψωτήρας με χρήση υγρού πυκνότητας\(ρ = \frac{10^3}{π} \frac{kg}{m^3}\), όπου τα δύο έμβολα \(Α_1\) και \(Α_2\) κυλινδρικού σχήματος έχουν ακτίνες \(r_1 = 1m\) και \(r_2 = 2m\). To έμβολο \(Α_1\) έχει μάζα \(m_1 = 1kg\) και το έμβολο \(Α_2\) έχει μάζα \(m_2=20kg\). Τοποθετούμε πάνω στο έμβολο \(Α_2\) ένα αυτοκίνητο μάζας \(m = 980kg\). Πόση κατακόρυφη δύναμη \(F_1\) πρέπει να ασκήσουμε στο έμβολο \(Α_1\) ώστε τα έμβολα να ισορροπούν στο ίδιο ύψος; Αυξάνοντας το μέτρο της ασκούμενης δύναμης μετακινούμε το έμβολο \(Α_1\) κατά \(h_1 = 1m\), φέρνοντάς το να ισορροπεί σε μια νέα θέση. Πόσα εκατοστά θα ανέβει το αυτοκίνητο; Ποια η τελική τιμή της δύναμης \(F_1\); Να υπολογιστούν τα έργα που παράγουν η ατμόσφαιρα και δύναμη \(F_1\). Θεωρούνται γνωστά η ατμοσφαιρική πίεση \(P_{ατμ} = 10^5 \frac{N}{m^2}\) και η επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\). Οι κινήσεις των εμβόλων γίνονται χωρίς τριβές και το έργο της μάζας του νερού που μετακινείται να θεωρηθεί αμελητέο.
Απάντηση:
blog comments powered by Disqus