Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2018
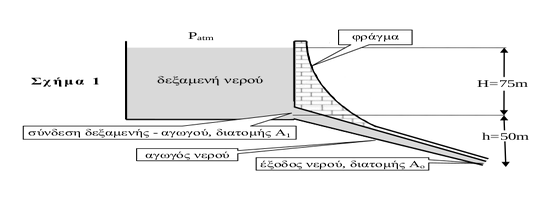
Στο σχήμα 1 δίνεται γράφημα ενός μεγάλου φράγματος που χρησιμοποιείται για την παραγωγή ηλεκτρικής ενέργειας. Το ύψος του νερού στη δεξαμενή του φράγματος είναι ίσο με \(H=75m\) και θεωρείται σταθερό, ενώ η υψομετρική διαφορά μεταξύ του σημείου εισόδου και του σημείου εξόδου στον αγωγό είναι ίση με \(h=50m\). Το νερό στο φράγμα θεωρείται ιδανικό ρευστό και έχει πυκνότητα \(ρ=1000\frac{kg}{m^3}\), η επιτάχυνση της βαρύτητας δίνεται \(g=10 \frac{m}{s^2}\) και η ατμοσφαιρική πίεση είναι ίση με \(P_{atm} =10^5 Pa\). Η διατομή του αγωγού στην έξοδο του νερού είναι ίση με \(Α_ο =1m^2\) , ενώ στο σημείο σύνδεσης δεξαμενής - αγωγού η διατομή του αγωγού είναι \(Α_1\).
1 Να βρεθεί η μάζα του νερού που εξέρχεται από τον αγωγό σε χρόνο \(t=1min\)
2 Αν στην έξοδο του αγωγού υπάρχει υδροστρόβιλος από τον οποίο το νερό εξέρχεται με ταχύτητα που είναι ίση με το 20% της ταχύτητας με την οποία το νερό φτάνει σε αυτόν, να βρεθεί η ηλεκτρική ισχύς \(P_{ηλ}\) που παράγεται από τον υδροστρόβιλο. Θεωρήστε ότι δεν παράγεται κανενός είδους θερμότητα.
3 Σε σημεία της μάζας του νερού στα οποία η πίεση είναι πολύ μικρή (θεωρήστε μηδενική) δημιουργούνται φυσαλίδες. Το φαινόμενο λέγεται σπηλαίωση (cavitation) και προκαλεί μείωση της μέσης πυκνότητας του νερού και προβλήματα απόδοσης και αντοχής των υλικών. Αν ο αγωγός νερού έχει σε όλο του το μήκος σταθερή διατομή ίση με \(Α_ο =1m^2\), να δείξετε ότι υπάρχει τουλάχιστον ένα σημείο στον αγωγό που εμφανίζει σπηλαίωση. Αν κατά τον σχεδιασμό του φράγματος και για την αποφυγή σπηλαίωσης τέθηκε κατώτατο όριο ασφαλείας της πίεσης του νερού \(P_{ασφ} =0,5 \cdot P_{atm}\), να βρεθεί η ελάχιστη διατομή \(Α_{1min}\) στην σύνδεση δεξαμενής - αγωγού. Η διατομή του αγωγού στην έξοδο του νερού παραμένει \(Α_ο =1m^2\)
4 Στην επιφάνεια του νερού στο φράγμα και σε σημεία \(Π_1\) και \(Π_2\) που απέχουν απόσταση \(d=4m\) μεταξύ τους, τοποθετούνται δυο σύγχρονες πηγές παραγωγής εγκαρσίων κυμάτων συχνότητας \(f=2Hz\). Αν μεταξύ των πηγών παρατηρούνται πέντε σημεία ενίσχυσης, τότε να βρεθεί η περιοχή των δυνατών τιμών της ταχύτητας διάδοσης των κυμάτων στην επιφάνεια του νερού.
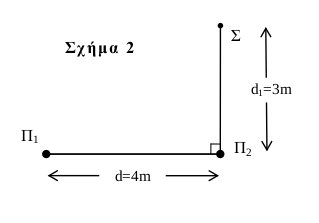
5 Τμήμα \(Π_2 Σ\) της επιφάνειας του νερού μήκους \(d_1 =3m\), είναι κάθετο στο τμήμα \(Π_1 Π_2\) που συνδέει τις σύγχρονες πηγές του παραπάνω ερωτήματος (σχήμα 2). Αν η ταχύτητα διάδοσης των κυμάτων στο νερό είναι ίση με \(υ=3 \frac{m}{s}\), να βρεθεί η συχνότητα των σύγχρονων πηγών \(Π_1\) και \(Π_2\) , ώστε στο τμήμα \(Π_2 Σ\) να δημιουργούνται δυο σημεία απόσβεσης, από τα οποία το ένα στο σημείο \(Σ\). Η συχνότητα των πηγών έχει αλλάξει και δεν είναι αυτή του ερωτήματος 4.
Απάντηση:
blog comments powered by Disqus