Επαναληπτικό διαγώνισμα στα ρευστά 2018 από study4exams
ΘΕΜΑ Α Στις προτάσεις \(Α_{1α}\) έως \(Α_{4β}\) να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά.
Α1α. Στον οριζόντιο σωλήνα του σχήματος ρέει ένα ιδανικό υγρό. Για τα σημεία 1 και 2 της ίδιας ρευματικής γραμμής ισχύει

α. \(υ_1=υ_2\) και \(p_1=p_2\)
β. \(υ_1>υ_2\) και \(p_1>p_2\)
γ. \(υ_1<υ_2\) και \(p_1>p_2\)
δ. \(υ_1<υ_2\) και \(p_1<p_2\)
Α1β. Σε ένα σωλήνα μεταβλητής διατομής που ρέει ιδανικό υγρό, όταν οι δυναμικές γραμμές πυκνώνουν, αυξάνεται
α. η παροχή του σωλήνα.
β. η ταχύτητα του υγρού.
γ. η πυκνότητα του υγρού.
δ. ο όγκος του υγρού ανά μονάδα χρόνου.
Α2α. Έχουμε ένα δοχείο που περιέχει υγρό πυκνότητας \(ρ\) και η ελεύθερη επιφάνεια του υγρού βρίσκεται σε επαφή με τον ατμοσφαιρικό αέρα. Η πίεση σε ένα σημείο του υγρού σε συνάρτηση με το βάθος \(y\) από την ελεύθερη επιφάνεια του υγρού, δίνεται από την γραφική παράσταση
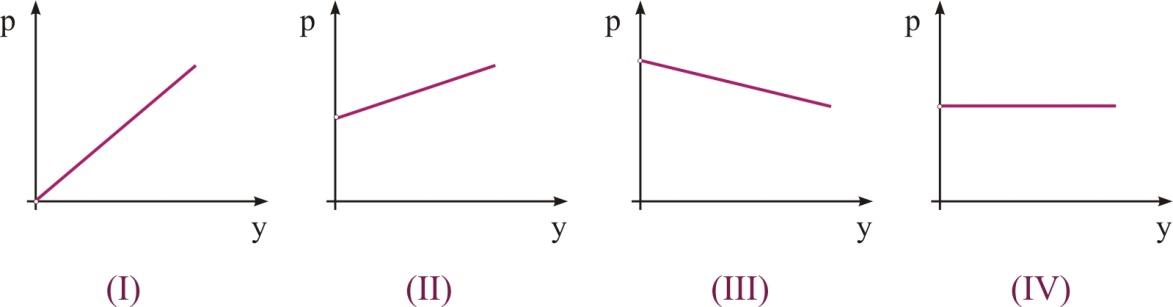
α) I
β) II
γ) III
δ) IV
Α2β. Ένα ανοικτό κυλινδρικό δοχείο με μεγάλο εμβαδό βάσης περιέχει νερό. Στο πλευρικό τοίχωμα του δοχείου και στην ίδια κατακόρυφο ανοίγουμε δύο μικρές οπές οι οποίες απέχουν από τη βάση του δοχείου \(h_1\) και \(h_2\) , όπου \(h_1=2 \cdot h_2\), όπως στο σχήμα. Για τα μέτρα των ταχυτήτων εκροής του νερού από τις δύο οπές ισχύει
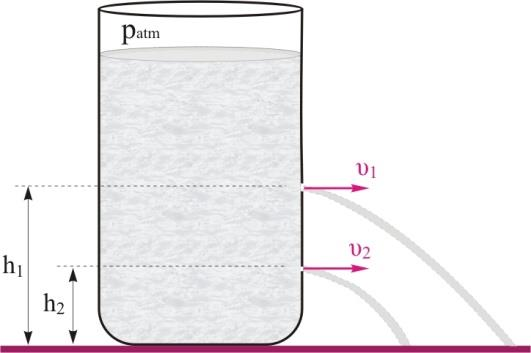
α. \(υ_1 =4 \cdot υ_2\)
β. \(υ_1 = υ_2\)
γ. \(υ_1 < υ_2\)
δ. \(υ_1 =2 \cdot υ_2\)
Α3α. Στο διπλανό σχήμα ανάμεσα στην πλάκα Π, εμβαδού \(Α\) και του επιπέδου υπάρχει ένα στρώμα από νευτώνειο υγρό πάχους \(d\). H πλάκα Π κινείται με σταθερή ταχύτητα \(υ\) όταν δέχεται οριζόντια δύναμη \(F\). Εάν η πλάκα είχε διπλάσιο βάρος τότε για να κινείται με την ίδια ταχύτητα \(υ\) θα πρέπει να του ασκηθεί οριζόντια δύναμη \(F_1\) για την οποία θα ισχύει

α) \(F_1= F\)
β) \(F_1 = 2 \cdot F\)
γ) \(F_1 = \frac{F}{2}\)
δ) δεν μπορούμε να γνωρίζουμε.
Α3β. Ρίχνουμε την ίδια ποσότητα νερού σε τρία κυλινδρικά δοχεία που έχουν εμβαδά βάσης \(Α, \quad 2\cdotΑ\) και \(3\cdotΑ\) αντίστοιχα. Οι υδροστατικές πιέσεις στις βάσεις των δοχείων είναι αντίστοιχα \(p_1, \quad p_2\) και \(p_3\) . Οι τρεις πιέσεις συνδέονται με τη σχέση
α) \(p_1 = p_2 = p_3\)
β) \(p_1 = p_2 >p_3\)
γ) \(p_1 < p_2 <p_3\)
δ) \(p_1 > p_2 >p_3\)
Α4α. Ιδανικό υγρό ρέει σε ένα πλάγιο σωλήνα που σχηματίζει γωνία με το οριζόντιο δάπεδο και παρουσιάζει στένωση, όπως στο σχήμα. Για τις παροχές του σωλήνα στις περιοχές \(1, \quad 2\) και \(3\) ισχύει
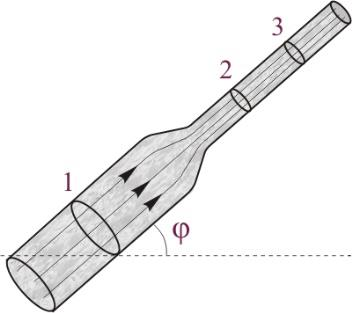
α) \(Π_1 > Π_2 > Π_3\)
β) \(Π_1 < Π_2 = Π_3\)
γ) \(Π_1 > Π_2 = Π_3\)
δ) \(Π_1 = Π_2 = Π_3\)
Α4β. H εξίσωση του Bernoulli για οποιαδήποτε σημεία της ίδιας ρευματικής γραμμής γράφεται
α) \(p+\frac{1}{2}ρ\cdot υ^2 + ρ \cdot g \cdot h = σταθερό\)
β) \(Α \cdot υ = σταθερό\)
γ) \(\frac{1}{2}ρ\cdot υ^2 + ρ \cdot g \cdot h = p\)
δ) \(p+\frac{1}{2}ρ\cdot υ^2 =ρ \cdot g \cdot h\)
Α5. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα τη λέξη Σωστό, για τη σωστή πρόταση, και τη λέξη Λάθος, για τη λανθασμένη.
α. Η υδροστατική πίεση σε ένα ορισμένο βάθος ενός υγρού είναι ανάλογη του βάθους, ανάλογη της πυκνότητας του υγρού και ανάλογη της επιτάχυνσης της βαρύτητας.
β. Ένας κύλινδρος επιπλέει εν μέρει βυθισμένος σε ένα υγρό. Η υδροστατική πίεση στη κάτω βάση του κυλίνδρου είναι ανάλογη του εμβαδού της βάσης του κυλίνδρου.
γ. Ασυμπίεστα θεωρούνται τα ρευστά των οποίων η πυκνότητα δε μεταβάλλεται αν μεταβληθεί η πίεσή τους για μια δεδομένη θερμοκρασία.
δ. Δύο ρευματικές γραμμές δεν μπορεί να τέμνονται γιατί στο σημείο τομής τους ένα μόριο του ρευστού θα είχε δύο ταχύτητες.
ε. Τα νευτώνεια υγρά συμπεριφέρονται σαν ιδανικά ρευστά.
ΘΕΜΑ Β Β1. Το δοχείο του σχήματος έχει μεγάλη διατομή και περιέχει νερό ύψους \(Η\) και πυκνότητας \(ρ\). Στο πυθμένα της δεξαμενής υπάρχει ένας οριζόντιος λεπτός σωλήνας. Το άκρο του \(Γ\) , είναι κλειστό και η πίεση του νερού στο σημείο \(Γ\) είναι \(p_1\). Αν ανοίξουμε το άκρο \(Γ\) του σωλήνα, το νερό εξέρχεται στην ατμόσφαιρα και η πίεση του νερού στο άκρο \(Γ\) γίνεται \(p_2\).
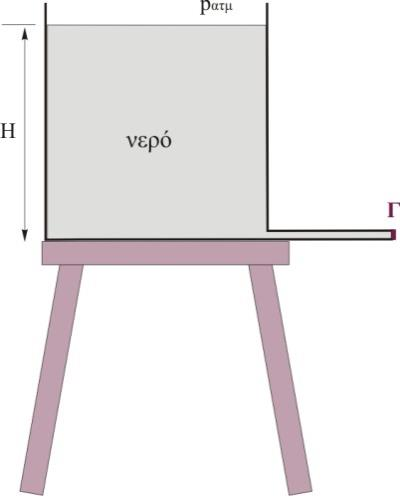
Η μεταβολή της πίεσης στο άκρο του σωλήνα \(Δ_p\), είναι ίση με
α. \(Δ_p=-ρ \cdot g \cdot H\)
β. \(Δ_p=+ρ \cdot g \cdot H\)
γ. \(Δ_p=-ρ \cdot g \cdot H+p_{atm}\)
Να επιλέξετε τη σωστή απάντηση.
Να δικαιολογήσετε την επιλογή σας.
Β2. Διαθέτουμε δύο όμοια κυλινδρικά δοχεία \(Α,\quadΒ\) στις βάσεις των οποίων υπάρχουν δύο όμοιες οπές με πολύ μικρό εμβαδό σε σχέση με το εμβαδό βάσης των δοχείων. Οι οπές είναι κλειστές με τάπες. Διαθέτουμε επίσης δύο υγρά με πυκνότητες \(ρ_1, \quad ρ_2\)με \(ρ_1 = 4\cdot ρ_2\). Τοποθετούμε τα υγρά στα δύο δοχεία όπως στο σχήμα, διαχωρισμένα μεταξύ τους με λεπτό αβαρές διάφραγμα που μπορεί να κινείται χωρίς τριβές. Το ύψος κάθε στήλης υγρού είναι ίσο με \(h\). Τη χρονική στιγμή \(t=0\) βγάζουμε ταυτόχρονα τις δύο τάπες από τα δοχεία. Αν με \(υ_Α, \quad υ_Β\) συμβολίσουμε τις ταχύτητες εκροής των δύο οπών, τη χρονική στιγμή \(t=0\) αυτές συνδέονται με τη σχέση
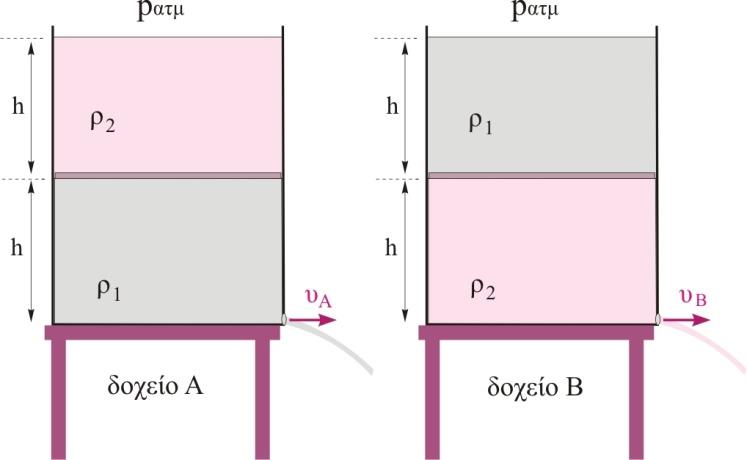
α) \(υ_A = υ_B\)
β) \(υ_A = 2 \cdot υ_B\)
γ) \(υ_B = 2 \cdot υ_A\)
Να επιλέξετε τη σωστή απάντηση.
Να δικαιολογήσετε την επιλογή σας.
Β3. Ένας γεωργός για να ελέγχει την παροχή νερού μέσα σε ένα σωλήνα άρδευσης κάνει το εξής. Σε ένα οριζόντιο τμήμα του σωλήνα που έχει στένωση προσαρμόζει δυο λεπτούς κατακόρυφους διαφανείς σωλήνες, όπως φαίνεται στο σχήμα. Όταν η παροχή του σωλήνα είναι \(Π_1\) , οι στήλες νερού στους κατακόρυφους σωλήνες παρουσιάζουν υψομετρική διαφορά \(Δh_1\). Αν η παροχή νερού μέσα στο σωλήνα διπλασιαστεί, οι στήλες νερού στους κατακόρυφους σωλήνες θα παρουσιάσουν υψομετρική διαφορά \(Δh_2\) για την οποία ισχύει
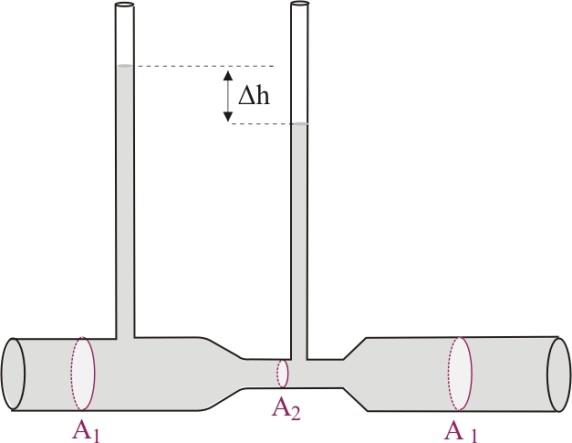
α) \(Δh_2 = Δh_1\)
β) \(Δh_2 =2Δh_1\)
γ) \(Δh_2 = 4Δh_1\)
Να επιλέξετε τη σωστή απάντηση.
Να δικαιολογήσετε την επιλογή σας.
Β4. Στο σωλήνα του σχήματος που είναι μεταβλητής διατομής ρέει ιδανικό υγρό. Η προσφερόμενη ενέργεια ανά μονάδα όγκου για τη μετακίνηση του υγρού από το τμήμα \(Α\) στο τμήμα \(Β\) είναι μικρότερη από την προκαλούμενη αύξηση της δυναμικής ενέργειας ανά μονάδα όγκου του υγρού. Οι διατομές \(Α_1\) και \(Α_2\) συνδέονται με τη σχέση
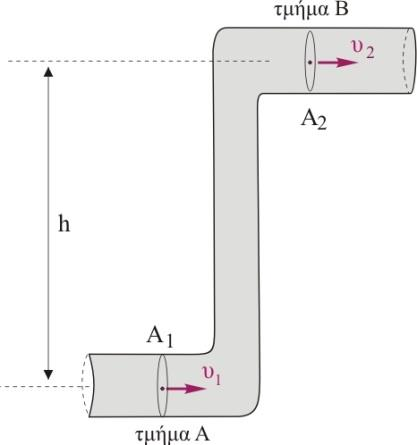
α) \(Α_1 = Α_2\)
β) \(Α_1 < Α_2\)
γ) \(Α_1 > Α_2\)
Να επιλέξετε τη σωστή απάντηση.
Να δικαιολογήσετε την επιλογή σας.
ΘΕΜΑ Γ Ένας μακρύς οριζόντιος σωλήνας με εμβαδό διατομής \(Α=0,06m^2\) βρίσκεται σε ύψος \(H\) πάνω από οριζόντιο δάπεδο, διαρρέεται από νερό και το δεξιό του άκρο είναι κλειστό. Ο σωλήνας έχει στο τέλος του δύο οπές με εμβαδά \(Α_1=10cm^2\), \(Α_2=20 cm^2\) κάτω από τις οποίες υπάρχουν δύο κυλινδρικά δοχεία με εμβαδά βάσης \(ΑA\) και \(ΑΒ=1,5 \cdot ΑA\) αντίστοιχα και ύψος \(h, \quad (h<Η)\). Οι βάσεις των δύο δοχείων συνδέονται μεταξύ τους με λεπτό οριζόντιο σωλήνα, ο οποίος διαθέτει διακόπτη \(δ\), που αρχικά είναι κλειστός. Η ταχύτητα εκροής του νερού από την οπή εμβαδού \(Α_1=10 cm^2\) είναι \(υ_1= 10\frac{m}{s}\)
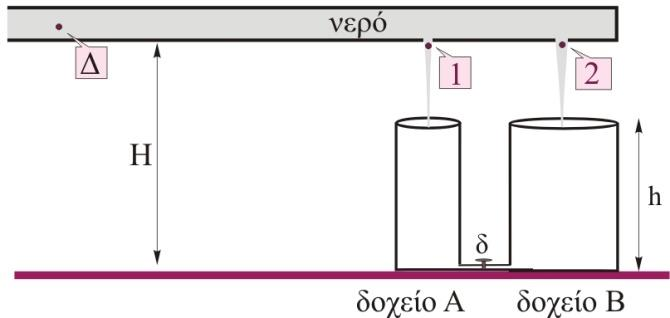
Γ1. Να βρείτε την ταχύτητα εκροής του νερού από την οπή εμβαδού \(Α_2=20 cm^2\)
Γ2. Να βρείτε την κινητική ενέργεια ανά μονάδα όγκου του νερού στα σημεία εκροής του από τις οπές.
Γ3. Να βρείτε το μέτρο της ταχύτητας του νερού στον οριζόντιο σωλήνα καθώς και την πίεση σε ένα εσωτερικό σημείο της περιοχής \(Δ\), αυτού.
Γ4. Όταν το ύψος του νερού στο πρώτο δοχείο είναι \(h_Α=1,2m\) διακόπτουμε την παροχή νερού και ανοίγουμε τον διακόπτη. Να βρεθεί τελικά σε τι ύψος θα φτάσει το νερό σε κάθε δοχείο.
Δίνονται: Η επιτάχυνση της βαρύτητας \(g=10 \frac{m}{s^2}\),η ατμοσφαιρική πίεση \(Ρ_{ατμ.}=10^5\frac{N}{m^2}\) και η πυκνότητα του νερού \(ρ=10^3\frac{Kg}{m^3}\). Θεωρούμε ότι το νερό είναι ιδανικό ρευστό.
ΘΕΜΑ Δ Μια ανοικτή κυλινδρική δεξαμενή με μεγάλη ακτίνα βάσης και ύψος \(Η=25m\) βρίσκεται σε οριζόντιο επίπεδο στην επιφάνεια της Γης και είναι γεμάτη με νερό. Στην πλευρική επιφάνεια της δεξαμενής και σε βάθος \(h_1=5m\) από την επιφάνεια του νερού υπάρχει μια μικρή οπή με εμβαδό \(Α_{οπ}= 5 cm^2\) η οποία είναι κλεισμένη με μια τάπα. Στο ίδιο οριζόντιο επίπεδο με τη βάση της δεξαμενής και σε απόσταση \(d=24m\) από τη δεξαμενή υπάρχει μια ακίνητη λεπτή κατακόρυφη δοκός ύψους \(h_{δοκού} =15m\) η οποία είναι στερεωμένη σε οδηγό , ο οποίος οδηγός μπορεί να κινείται στο οριζόντιο επίπεδο διατηρώντας τη δοκό διαρκώς κατακόρυφη. Τη χρονική στιγμή \(t_o=0\) αφαιρούμε την τάπα από την οπή και ταυτόχρονα επιταχύνουμε τη δοκό με σταθερή επιτάχυνση, \(α_1\), προς τη δεξαμενή. Tη χρονική στιγμή \(t_1\), η πρώτη σταγόνα νερού που φτάνει στο έδαφος συναντά τη δοκό στο χαμηλότερο σημείο της \(Γ\). Στη συνέχεια επιβραδύνουμε ομαλά τη δοκό με επιτάχυνση \(α_2\) και αυτή σταματά τη χρονική στιγμή \(t_2\) σε μια θέση όπου η φλέβα νερού περνά οριακά πάνω από ψηλότερο σημείο της δοκού \(Β\). Να βρείτε:
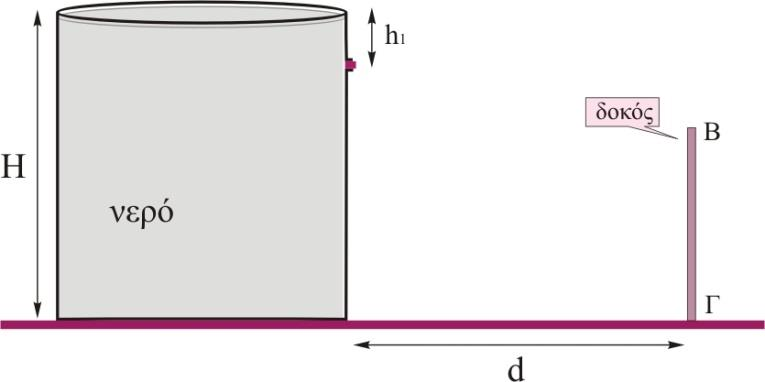
Δ1. την ταχύτητα του νερού τη στιγμή που φτάνει στο έδαφος (μέτρο και κατεύθυνση).
Δ2. το εμβαδόν \(A\), της κάθετης διατομής της φλέβας λίγο πριν αυτή φτάσει στο έδαφος.
Δ3. την επιτάχυνση \(α_1\) της δοκού.
Δ4. την επιτάχυνση \(α_2\) της δοκού και να σχεδιάσετε σε αριθμημένους άξονες το διάγραμμα της ταχύτητας της δοκού σε συνάρτηση με το χρόνο από τη στιγμή \(t=0\) μέχρι τη στιγμή \(t=10s\).
Δίνονται: Η επιτάχυνση της βαρύτητας \(g=10\frac{m}{s^2}\), η ατμοσφαιρική πίεση \(Ρ_{ατμ.}=10^5\frac{N}{m^2}\) , η πυκνότητα του νερού \(ρ_{νερού}=10^3\frac{Kg}{m^3}\) και ότι σε όλη τη διάρκεια του φαινομένου το ύψος του νερού στη δεξαμενή παραμένει σταθερό.
Θέμα Α
Α1α - \(γ\)
Α1β - \(β\)
Α2α - \(β\)
Α2β - \(γ\)
Α3α - \(α\)
Α3β - \(δ\)
Α4α - \(δ\)
Α4β - \(α\)
Α5: \(Σ - Λ - Σ - Σ - Λ\)
Θέμα Β
B1-\((α)\)
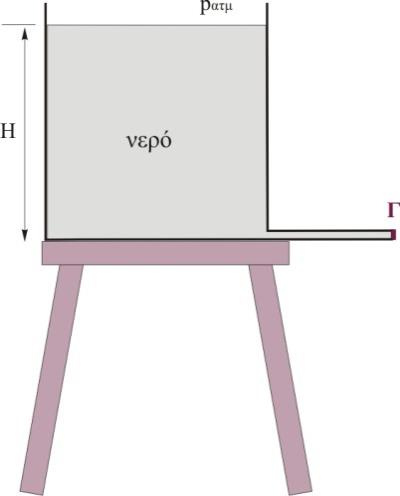
Αρχικά το νερό ισορροπεί οπότε
\[p_1 = p_Γ = p_{ατμ} + ρ \cdot g \cdot H\]Όταν ανοίξουμε το άκρο \(Γ\) του σωλήνα η πίεση γίνεται
\[p_2 = p_Γ = p_{ατμ}\] \[Δp = p_2 - p_1 = - ρ \cdot g \cdot H\]άρα σωστό το (α)
Β2 - \((γ)\)
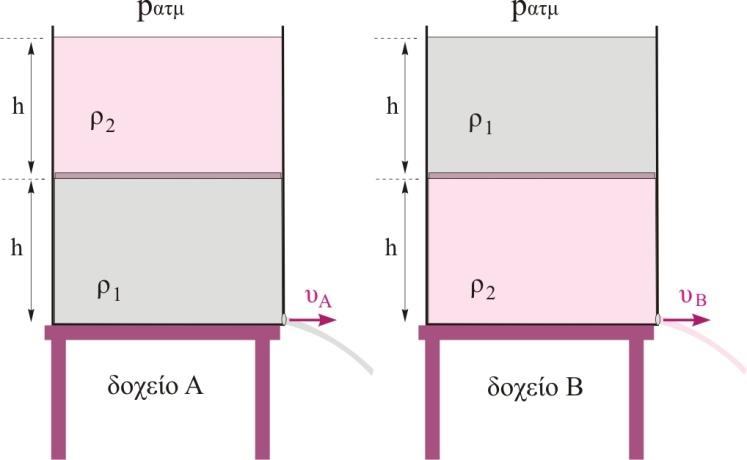
Εφαρμόζουμε την εξίσωση του Bernoulli για το δοχείο Α, από το σημείο \(Γ\) στο λεπτό αβαρές διάφραγμα στο σημείο \(Α\) δηλαδή την τάπα του δοχείου.
\[p_Γ + \frac{1}{2} \cdot ρ_1 \cdot υ_Γ^2 + ρ_1 \cdot g \cdot h = p_{ατμ} + \frac{1}{2} \cdot ρ_1 \cdot υ_Α^2 + ρ_1 \cdot g \cdot 0 \Rightarrow p_{ατμ} + ρ_2 \cdot g \cdot h + 0 + ρ_1 \cdot g \cdot h = p_{ατμ} + \frac{1}{2} \cdot ρ_1 \cdot υ_Α^2\]και κάνοντας τις πράξεις έχουμε τελικά
\[υ_Α = \sqrt{\frac{2\cdot g \cdot h \cdot (ρ_1+ρ_2)}{ρ_1}}\]Με τον ίδιο τρόπο εφαρμόζουμε την εξίσωση του Bernoulli για το δοχείο Β, οπότε για την ταχύτητα \(υ_Β\) προκύπτει:
\[υ_Β = \sqrt{\frac{2\cdot g \cdot h \cdot (ρ_1+ρ_2)}{ρ_2}}\]Και επειδή ισχύει \(ρ_1 = 4 \cdot ρ_2\) έχουμε
\[\frac{υ_Α}{υ_Β} = \sqrt{\frac{ρ_2}{ρ_1}} \Rightarrow υ_Β = 2 \cdot υ_Α\]άρα σωστό το (γ)
Β3 - \((γ)\)
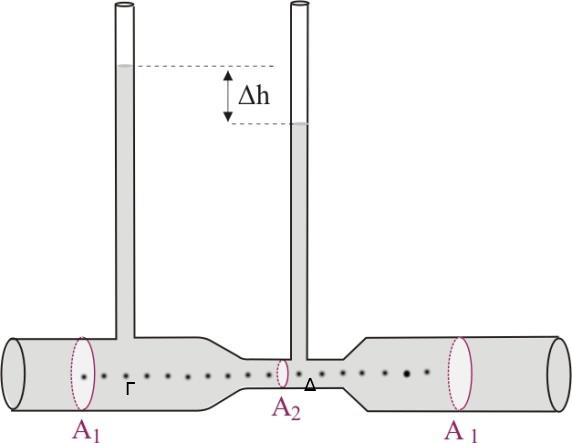
Θεωρούμε το νερό ασυμπίεστο ρευστό και την ροή στρωτή, οπότε ισχύει
\[Π_1 = Α_1 \cdot υ_1 = Α_2 \cdot υ_2 \Rightarrow υ_2 = \frac{A_1}{A_2} \cdot υ_1\]Εφαρμόζουμε την εξίσωση του Bernoulli στα σημεία \(Γ\) και \(Δ\)
\[p_Γ + \frac{1}{2} \cdot ρ \cdot υ_1^2 = p_Δ + \frac{1}{2} \cdot ρ \cdot υ_2^2 \Rightarrow p_{ατμ} +ρ \cdot g \cdot h_1 + \frac{1}{2} \cdot ρ \cdot υ_1^2 = p_{ατμ} + ρ \cdot g \cdot h_2 + \frac{1}{2} \cdot ρ \cdot υ_2^2\] \[ρ \cdot g \cdot (h_1 - h_2) = \frac{1}{2} \cdot ρ \cdot (υ_2^2 - υ_1^2) \Rightarrow Δh_1 = \frac{1}{2g} \cdot (υ_2^2 - υ_1^2)\] \[Δh_1 = \frac{1}{2g} \cdot (\frac{A_1^2}{A_2^2} - 1) \cdot υ_1^2\]Όταν διπλασιάζεται η παροχή, εφόσον παραμένει ίδιο το εμβαδό διατομής του σωλήνα διπλασιάζεται η ταχύτητα, δηλαδή
\[υ_1' = 2 \cdot υ_1\]Ομοίως εφαρμόζουμε την εξίσωση Bernoulli στα σημεία \(Γ\) και \(Δ\) και έχουμε τελικά
\[Δh_2 = \frac{1}{2g} \cdot (\frac{A_1^2}{A_2^2} - 1) \cdot υ_1'^2 \Rightarrow Δh_2 = 4 \cdot Δh_1\]άρα σωστό το (γ)
Β4 - \((β)\)
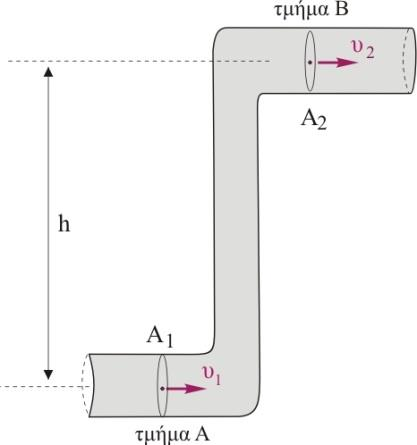
Εφαρμόζουμε το θεώρημα Μεταβολής της Κινητικής Ενέργειας για τμήμα ρευστού \(Δm\) από το σημείο \(Α\) στο σημείο \(Β\).
\[ΔΚ = ΣW \Rightarrow K_B - K_A = W_F + W_B \Rightarrow \frac{1}{2} \cdot Δm (υ_2^2 - υ_1^2) = W_F + W_B\]διαιρούμε και τα δύο μέλη της εξίσωσης με τον στοιχειώδη όγκο \(ΔV\)
\[\frac{1}{2} \cdot \frac{Δm}{ΔV} \cdot (υ_2^2 - υ_1^2) = \frac{W_F}{ΔV} + \frac{W_B}{ΔV}\]από τα δεδομένα γνωρίζουμε ότι
\[\frac{W_F}{ΔV} < \frac{ΔU}{ΔV} = - \frac{W_B}{ΔV} \Rightarrow \frac{W_F}{ΔV} + \frac{W_B}{ΔV} < 0\]οπότε από την προηγούμενη εξίσωση συμπεραίνουμε ότι
\[υ_2 < υ_1\]και επειδή κατά μήκος του σωλήνα η παροχή διατηρείται έχουμε:
\[Π_Α = Π_Β \Rightarrow A_1 \cdot υ_1 = Α_2 \cdot υ_2 \Rightarrow \frac{A_1}{A_2} = \frac{υ_2}{υ_1} \Rightarrow A_1 < A_2\]Θέμα Γ
Γ1
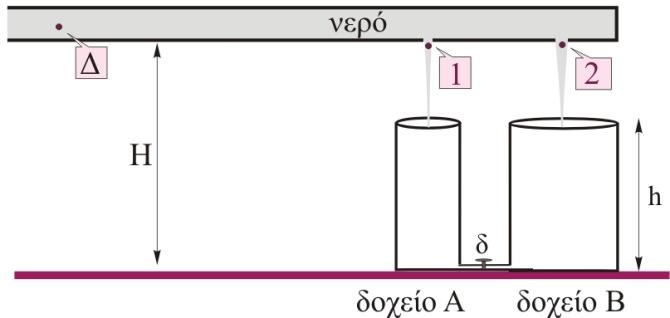
Εφαρμόζουμε την εξίσωση του Bernoulli στα σημεία \(Δ\) και \(Α_1\)
\[p_Δ + \frac{1}{2} \cdot ρ \cdot υ^2 = p_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_1^2\]ομοίως στα σημεία \(Δ\) και \(Α_2\)
\[p_Δ + \frac{1}{2} \cdot ρ \cdot υ^2 = p_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_2^2\]από όπου συμπεραίνουμε ότι
\[υ_1 = υ_2 = 10 \frac{m}{s}\]Γ2
\[\frac{ΔΚ_1}{ΔV} = \frac{ΔΚ_2}{ΔV} = \frac{1}{2} ρ \cdot υ_1^2 = 5 \cdot 10^4 \frac{Joule}{m^3}\]Γ3
Επειδή το άκρο του σωλήνα είναι κλειστό ισχύει
\[Π_Δ = Π_1 + Π_2 \Rightarrow A \cdot υ = A_1 \cdot υ_1 + Α_2 \cdot υ_2 \Rightarrow υ = 0.5 \frac{m}{s}\] \[p_Δ + \frac{1}{2} \cdot ρ \cdot υ^2 = p_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_1^2 \Rightarrow p_Δ = 149875 \frac{N}{m^2}\]Γ4
\[Π_1 = \frac{ΔV_1}{Δt} \Rightarrow Δt = \frac{ΔV_1}{Π_1} \Rightarrow Δt = \frac{A_A \cdot h_A}{A_1 \cdot υ_1} \Rightarrow Δt = 120 \cdot A_A\]Στον ίδιο χρόνο για το δοχείο \(Β\) ισχύει:
\[Δt = \frac{ΔV_2}{Π_2} \Rightarrow Δt = \frac{1.5 \cdot A_A \cdot h_B}{Π_2}\]από όπου υπολογίζουμε το ύψος στο δοχείο \(Β\)
\[h_B = 1.6 m\]Αφού ανοίξουμε τον διακόπτη, τα δοχεία είναι συγκοινωνούντα άρα
\[Α_Α \cdot h_A + A_B \cdot h_B = (A_A + A_B) \cdot h \Rightarrow h = 1.44 m\]Θέμα Δ
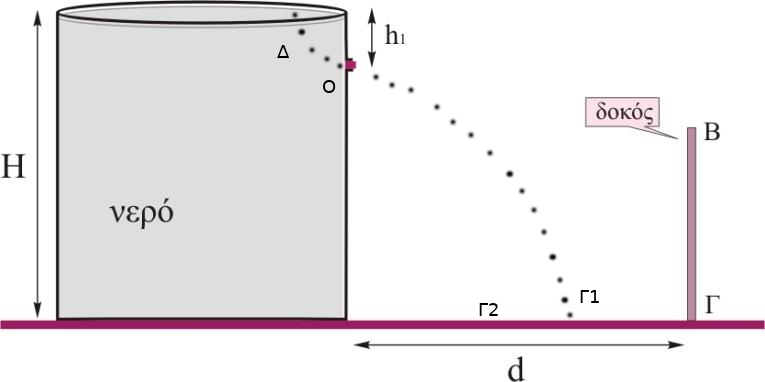
Δ1
Εφαρμόζουμε την εξίσωση Bernoulli στα σημεία \(Δ\), \(Ο\) και \(Γ_1\) για τη ρευματική γραμμή που φαίνεται στο παραπάνω σχήμα.
\[p_{ατμ} + 0 + ρ \cdot g \cdot H = p_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_ο^2 + ρ \cdot g \cdot (H - h_1) = p_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_1^2 + 0\] \[ρ \cdot g \cdot Η = \frac{1}{2} \cdot ρ υ_1^2 \Rightarrow υ_1 = 10 \sqrt5 \frac{m}{s}\] \[ρ \cdot g \cdot h_1 = \frac{1}{2} \cdot ρ υ_o^2 \Rightarrow υ_0 = 10 \frac{m}{s}\] \[συνφ = \frac{υ_ο}{υ} = \frac{\sqrt5}{5}\]Δ2
Θεωρούμε το νερό ασυμπίεστο ρευστό και την ροή στρωτή, οπότε ισχύει
\[Π_ο = Π_1 \Rightarrow Α_ο \cdot υ_ο = Α_1 \cdot υ_1 \Rightarrow Α_1 = \frac{A_ο \cdot υ_ο}{υ_1} \Rightarrow A_1 = 10^{-4} m^2\]Δ3
Για την κίνηση του στοιχειώδους ρευστού \(Δm\) από την θέση \(Ο\) στη θέση \(Γ_1\) ισχύει
\[Η - h_1 = \frac{1}{2} \cdot g \cdot t_{ΟΓ1}^2 \Rightarrow t_{ΟΓ1} = 2s\]Το στοιχειώδες ρευστό τη στιγμή που φτάνει στο έδαφος έχει διανύσει απόσταση
\[d - x_{Δ1} = υ_ο \cdot t_{ΟΓ1} \Rightarrow x_{Δ1} = 4 m\]Στον ίδιο χρόνο η δοκός κινείται από τη θέση \(Γ\) στη θέση \(Γ1\) κατά \(x_{Δ1}\)
\[x_{Δ1} = \frac{1}{2} \cdot α_1 \cdot t_{ΟΓ1}^2 \Rightarrow α_1 = 2 \frac{m}{s^2}\] \[υ_{Δ1} = α_1 \cdot t_{ΟΓ1} = 4 \frac{m}{s}\]Δ4
Για την κίνηση του στοιχειώδους ρευστού \(Δm\) από την θέση \(Ο\) στη θέση \(Β\) ισχύει
\[(Η - h_1) - h_{δοκου} = \frac{1}{2} \cdot g \cdot t_{ΟΒ}^2 \Rightarrow t_{ΟΒ} = 1 s\]Σε χρόνο \(t_{OB}\) το στοιχειώδες ρευστό κινείται στον οριζόντιο άξονα κατά
\[x = υ_ο \cdot t_{OB} = 10 m\] \[d = x + (Γ_2 Γ_1) + x_{Δ1} \Rightarrow (Γ_2 Γ_1) = 10 m\]και για την επιβραδυνόμενη κίνηση έχουμε
\[0 = υ_{Δ1} - α_2 \cdot t_{Γ2Γ1}\] \[(Γ_2 Γ_1) = υ_{Δ1} \cdot t_{Γ2Γ1} - \frac{1}{2} \cdot α_2 t_{Γ2Γ1}^2\]λύνοντας το σύστημα δύο εξισώσεων με δύο αγνώστους έχουμε
\[α_2 = 0.8 \frac{m}{s^2}\]και
\[t_{Γ2Γ1} = 5 s\]H γραφική παράσταση φαίνεται στην παρακάτω εικόνα
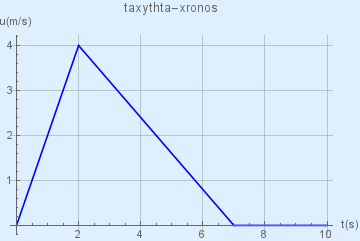
και ο κώδικας σε mathematica
f[t] := 2t
h[t] := 4 - 0.8*(t-2)
g[t] := 0
Show[{Plot[f[t], {t, 0, 2}, PlotStyle -> Blue],
Plot[h[t], {t, 2, 7}, PlotStyle -> Blue],
Plot[g[t], {t, 7, 10}, PlotStyle -> Blue]},
PlotRange -> All,
GridLines -> Automatic,
Background -> LightBlue,
PlotLabel -> "taxythta-xronos",
AxesLabel -> {"t(s)","u(m/s)"},
AxesOrigin -> {0, 0},
Filling -> Automatic]
blog comments powered by Disqus