S.T.E.M.

Εξαναγκασμένη ταλάντωση σε άσκηση του σχολικού βιβλίου

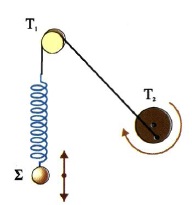
σχήμα

Το κατακόρυφο ελατήριο σταθεράς \(k = π^2 \frac{N}{m}\) του σχήματος είναι δεμένο με σχοινί, το άλλο άκρο του οποίου προσδένεται στον τροχό \(Τ_2\), ο οποίος με κατάλληλη διάταξη μπορεί να περιστρέφεται. Αρχικά ο τροχός είναι ακίνητος και το σώμα \(Σ\) μάζας \(4kg\) εκτελεί απλή αρμονική ταλάντωση με εξίσωση απομάκρυνσης \(y = 0.2 \cdot ημ(ω_o \cdot t)\) (μονάδες στο S.I.).

α) Να γίνει η γραφική παράσταση των χρονικών συναρτήσεων της Κινητικής και της Δυναμικής Ενέργειας ταλάντωσης.

Περιστρέφουμε τον τροχό \(Τ_2\) έτσι ώστε μια ακτίνα του να διαγράφει γωνία \(45^ο\) κάθε δευτερόλεπτο. Η περιστροφή του τροχού αναγκάζει το σφαιρίδιο να εκτελεί κατακόρυφη ταλάντωση. Η συχνότητα της ταλάντωσης συμπίπτει με τη συχνότητα περιστροφής του τροχού. Το σώμα δέχεται ταυτόχρονα από το περιβάλλον του μια δύναμη απόσβεσης της μορφής \(F = -b \cdot υ\). Το πλάτος της εξαναγκασμένης ταλάντωσης είναι \(Α = 0.2m\) και η αρχική της φάση \(φ=0\).

β) Να βρεθούν οι εξισώσεις \(υ=υ(t)\) και \(α=α(t)\) της ταχύτητας και της επιτάχυνσης του σώματος σε συνάρτηση με το χρόνο.

γ) Να βρεθούν οι εξισώσεις της κινητικής και της δυναμικής ενέργειας σε συνάρτηση με το χρόνο και να παρασταθούν γραφικά στους ίδιους άξονες.

δ) Το άθροισμα Κ+U των δύο παραπάνω ενεργειών παραμένει σταθερό στη διάρκεια της ταλάντωσης;

Δίνεται ότι \(π^2 \approx 10\)

Απάντηση:

\[Κ = 0.2 \cdot συν^2(\frac{π}{2} t), U = 0.2 \cdot ημ^2(\frac{π}{2} t)\]

Ο κώδικας σε mathematica

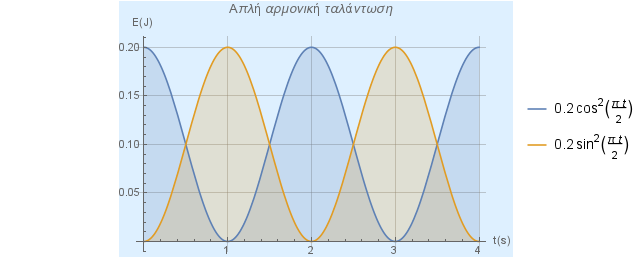
			Plot[{0.2*Cos[Pi*t/2]^2, 0.2*Sin[Pi*t/2]^2}, {t, 0, 4}, 
					PlotLegends ->"Expressions",  
					PlotRange -> All, 
					PlotLabel -> "Απλή Αρμονική Ταλάντωση", 
					Background -> LightBlue, 
					GridLines -> Automatic, 
					AxesLabel -> {"t(s)", "E(J)"}, 
					Filling -> Automatic]

και το αποτέλεσμα

σχήμα

\[υ = \frac{0.1 \cdot π}{2} συν(\frac{π}{4} t), α = - \frac{0.1 \cdot π^2}{8} ημ(\frac{π}{4} t)\] \[Κ = 0.05 \cdot συν^2(\frac{π}{4} t), U = 0.2 \cdot ημ^2(\frac{π}{4} t)\]

Ο κώδικας σε mathematica

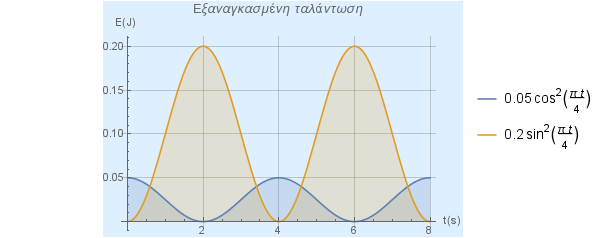
			Plot[{0.05*Cos[Pi*t/4]^2, 0.2*Sin[Pi*t/4]^2}, {t, 0, 8}, 
					PlotLegends ->"Expressions",  
					PlotRange -> All, PlotLabel -> "Εξαναγκασμένη Ταλάντωση", 
					Background -> LightBlue, 
					GridLines -> Automatic, 
					AxesLabel -> {"t(s)", "E(J)"}, 
					Filling -> Automatic]

και το αποτέλεσμα

σχήμα

\[όχι\]
blog comments powered by Disqus

Published

01 September 2017

Category

Άσκηση

Tags