Δυνάμεις σε πάσσαλο
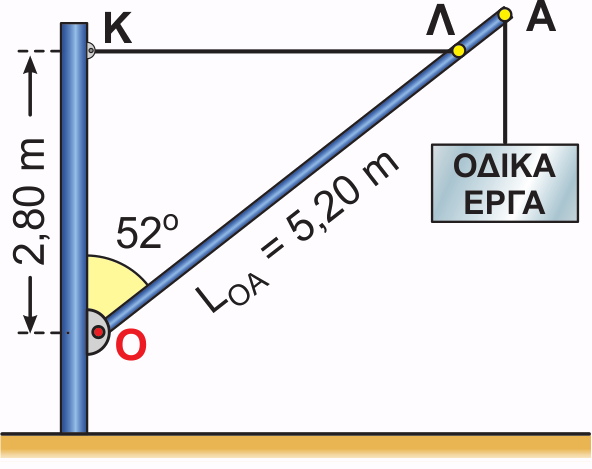
Το σχήμα απεικονίζει έναν πάσσαλο \(OA\) μάζας \(m_Π = 24.0 kg\), από τον οποίο έχει αναρτηθεί ένα σήμα τροχαίας με μάζα \(m_Σ = 8.0 kg\). Να υποθέσετε ότι ο πάσσαλος είναι ομογενής και βρίσκεται σε στατική ισορροπία. Να υπολογίσετε την τάση στο σημείο \(Λ\) του πασσάλου από το συρματόσχοινο \(ΚΛ\), και τη δύναμη στο σημείο \(Ο\) από τον κατακόρυφο στύλο. Δίνεται η επιτάχυνση της βαρύτητας \(g = 10\frac{m}{s^2}\)
Απάντηση:
Εάν το σήμα της τροχαίας είναι το σύστημα που μελετάμε το περιβάλλον για αυτό το σύστημα είναι η γη (δύναμη εξ’ αποστάσεως το βάρος \(m_Σ \cdot g\)) και το νήμα (δύναμη εξ’ επαφής, η τάση του νήματος \(Τ_1\)). Λόγω ισορροπίας αυτές οι δυνάμεις είναι ίσες.
\[ΣF = 0 \Rightarrow T_1 = m_Σ \cdot g \Rightarrow T_1 = 80N\]Εάν ο πάσσαλος είναι το σύστημα που μελετάμε το περιβάλλον για αυτό το σύστημα αποτελούν, η γη \(m_Π \cdot g\), το κατακόρυφο νήμα \(Τ_1\), το συρματόσχοινο \(Τ_2\) και ο κατακόρυφος στύλος, δυνάμεις \(F_x\) και \(F_y\). Λόγω της στατικής ισορροπίας το αλγεβρικό άθροισμα των ροπών ως προς το σημείο \(Ο\) για τον πάσσαλο είναι μηδέν.
\[Στ_{(Ο)} = 0 \Rightarrow τ_Β + τ_{Τ1} = τ_{Τ2} \Rightarrow m_Π \cdot g \cdot \frac{L}{2} \cdot ημ52^0 + Τ_1 \cdot L \cdot ημ52^0 = Τ_2 \cdot 28\]και κάνοντας αντικαταστάσεις έχουμε τελικά
\[Τ_2 = 292,7Ν\]Για να υπολογίσουμε τη δύναμη που ασκεί στον πάσσαλο ο κατακόρυφο στύλος έχουμε λόγω της στατικής ισορροπίας
\[ΣF_x = 0 \Rightarrow F_x - T_2 = 0 \Rightarrow F_x = 292,7N\] \[ΣF_y = 0 \Rightarrow F_y = m_Π \cdot g + T_1 \Rightarrow F_y = 320N\]Το μέτρο της συνισταμένης δύναμης είναι:
\[F = \sqrt{F_x^2 + F_y^2} \Rightarrow F = 433,6N\]η γωνία που σχηματίζει η δύναμη με τον ορίζοντα είναι
\[εφθ = \frac{F_y}{F_x} \Rightarrow θ = 47,5^0\]blog comments powered by Disqus