Θεμελιώδης νόμος της στροφικής κίνησης
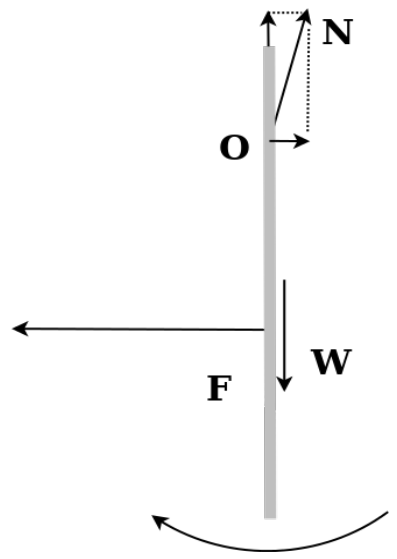
Ομογενής ράβδος μήκους \(l = 1m\) και μάζας \(M = 3 kg\) μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο σταθερό άξονα ο οποίος διέρχεται από σημείο Ο της ράβδου και είναι κάθετος στο επίπεδο περιστροφής της. Το σημείο Ο δεν είναι το κέντρο μάζας της ράβδου. \(ΟΑ = \frac{l}{5}\). Αρχικά η ράβδος ισορροπεί στην κατακόρυφη θέση όπως φαίνεται στο παρακάτω σχήμα. Την χρονική στιγμή \(t = 0s\) ασκούμε δύναμη \(F\) κάθετη στη ράβδο στο σημείο Κ το οποίο απέχει από το Ο απόσταση
\(x_1 = \frac{2 \cdot l}{5}\).
Η ράβδος ξεκινά να περιστρέφεται με αρχική γωνιακή επιτάχυνση
\(α_{γων} = 10 \frac{r}{s^2}\),
ενώ η δύναμη συνεχίζει να ασκείται στο σημείο Κ κάθετα στην ράβδο.
1) Να υπολογίσεται την ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το σημείο Ο και το μέτρο της δύναμης \(F\).
2) Να βρείτε το μέτρο της συνισταμένης δύναμης που δέχεται η ράβδος από τον άξονα περιστροφής της την χρονική στιγμή \(t = 0s\).
3) Να βρείτε την γωνιακή ταχύτητα της ράβδου την χρονική στιγμή που σχηματίζει με την κατακόρυφο γωνία \(θ = \frac{π}{4} rad\).
Θεωρήστε δεδομένα την επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\) και την ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το μέσο της και είναι κάθετος σε αυτή \(I = \frac{1}{12} \cdot M \cdot l^2\).
Απάντηση:
1) Κάνοντας χρήση του θεωρήματος Steiner έχουμε για την ροπή αδράνειας
\[Ι = 0,52 kg \cdot m^2\]Ενώ χρησιμοποιώντας τον βασικό νόμο της στροφικής κίνησης βρίσκουμε την δύναμη \(F = 13N\).
2) Για την συνισταμένη δύναμη που δέχεται η ράβδος από τον άξονα περιστροφής της την χρονική στιγμή \(t = 0s\), υπολογίζουμε πρώτα την οριζόντια συνιστώσα της με την βοήθεια του δεύτερου νόμου του Νεύτωνα και θεωρώντας ότι όλη η μάζα της ράβδου είναι συγκεντρωμένη στο κέντρο μάζας της
\[N_x = 1N\]και στην συνέχεια την κατακόρυφη συνιστώσα της με χρήση της σχέσης που υπολογίζει την κεντρομόλο δύναμη
\[N_y = 30N\]Οπότε για την συνισταμένη έχουμε \(Ν = \sqrt{901}\) με \(εφθ = 30\).
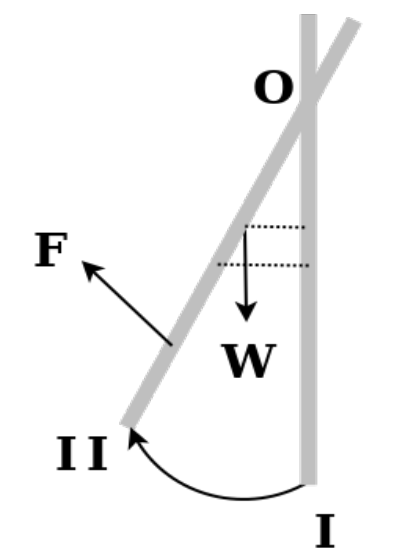
3) Εφαρμόζουμε το θεώρημα μεταβολής της κινητικής ενέργειας για την κίνηση της ράβδου από την θέση Ι στην θέση ΙΙ. Θεωρούμαι ως επίπεδο μηδενική ενέργειας αυτό που διέρχεται από το κέντρο μάζας της ράβδου στην θέση Ι. Το έργο του βάρους μπορεί να υπολογιστεί από την σχέση
\[W = U_{αρχ} - U{τελ}\]και είναι αρνητικό, ενώ το έργο της ροπής της δύναμης \(F\) από την σχέση
\[W = F \cdot x_1 \cdot \frac{π}{4}\]και είναι θετικό, οπότε τελικά μετά τις πράξεις έχουμε για την γωνιακή ταχύτητα την τιμή \(ω = 2.36 \frac{r}{s}\).
blog comments powered by Disqus