Ισορροπία δοκού
Ομογενής και ισοπαχής μεταλλική δοκός \(ΟΓ\) έχει βάρος \(200Ν\) και μήκος \(L=4m\). Η δοκός στηρίζεται σε δύο υποστηρίγματα \(Δ_1\) και \(Δ_2\) τα οποία απέχουν από το άκρο της Ο αποστάσεις \(d_1=0.5m\) και \(d_2=3m\) αντίστοιχα.
α) Ένα μικρό παιδί μάζας \(m=25kg\) στέκεται ακίνητο στο αριστερό άκρο της δοκού Ο, χωρίς αυτή να ανατρέπεται. Να υπολογίσετε τα μέτρα των δυνάμεων που δέχεται η δοκός από τα υποστηρίγματα \(Δ_1\) και \(Δ_2\) ξεχωριστά.
β) Nα βρείτε την εξίσωση η οποία δίνει το μέτρο της δύναμης που δέχεται η δοκός από το υποστήριγμα \(Δ_1\), όπως και την εξίσωση της δύναμης που δέχεται από το υποστήριγμα \(Δ_2\), σε συνάρτηση με την θέση \(x\) του παιδιού ως προς το άκρο \(Ο (x=0)\) της δοκού και να εξετάσετε αν υπάρχουν κάποιες θέσεις πάνω στη δοκό στις οποίες αν βρεθεί το παιδί η δοκός θα ανατραπεί. Δίνεται η επιτάχυνση της βαρύτητας \(g=10 \frac{m}{s^2}\).
Απάντηση:
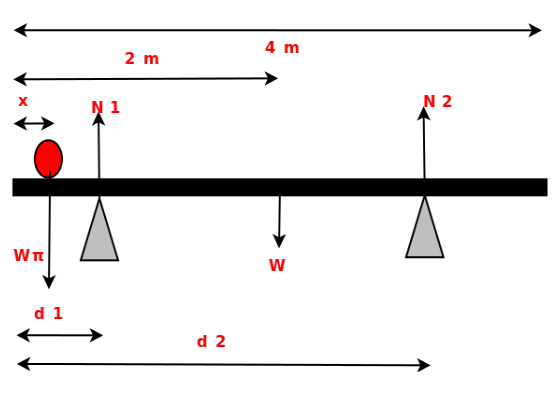
α)Η δοκός ισορροπεί και το μικρό παιδί βρίσκεται στο άκρο Ο της δοκού. Άρα
\[ΣF_y = 0 \Rightarrow N_1 +N_2 = W_Π + W \Rightarrow N_1 +N_2 = 450\]Το αλγεβρικό άθροισμα των ροπών ως προς το υποστήριγμα \(Δ_1\) είναι
\[Στ = 0 \Rightarrow W_Π \cdot d_1 + N_2 \cdot (d_2 - d_1) - W \cdot (\frac{L}{2}-d_1) = 0\]και μετά τις πράξεις έχουμε:
\[N_1 = 380N, N_2 = 70N\]β) Όταν το μικρό παιδί βρίσκεται αριστερά του πρώτου υποστηρίγματος δηλαδή για \(0 \le x \le 0.5\) έχουμε:
\[ΣF_y = 0 \Rightarrow N_1 +N_2 = W_Π + W \Rightarrow N_1 +N_2 = 450\]Το αλγεβρικό άθροισμα των ροπών ως προς το υποστήριγμα \(Δ_1\) είναι
\[Στ = 0 \Rightarrow W_Π \cdot (d_1-x) + N_2 \cdot (d_2 - d_1) - W \cdot (\frac{L}{2}-d_1) = 0\]και μετά τις πράξεις έχουμε:
\[N_1 = 380 - 100 \cdot x\] \[N_2 = 70 + 100 \cdot x\]όταν το μικρό παιδί βρίσκεται δεξιά του πρώτου υποστηρίγματος δηλαδή για \(0.5 \le x \le 4\) έχουμε:
\[Στ = 0 \Rightarrow -250 \cdot (x - 0.5) + N_2 \cdot 2.5 -300 =0\]και τελικά μετά τις πράξεις έχουμε:
\[N_1 = 380 - 100 \cdot x\] \[N_2 = 70 + 100 \cdot x\]Η επαφή χάνεται μόνο για το πρώτο υποστήριγμα, και αυτό συμβαίνει όταν το μικρό παιδί βρίσκεται δεξιά του πρώτου υποστηρίγματος δηλαδή για \(0.5 \le x \le 4\)
\[Ν_1 \ge 0 \Rightarrow 380 - 100 \cdot x \ge 0 \Rightarrow x \le 3.8 m\]blog comments powered by Disqus