Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2013
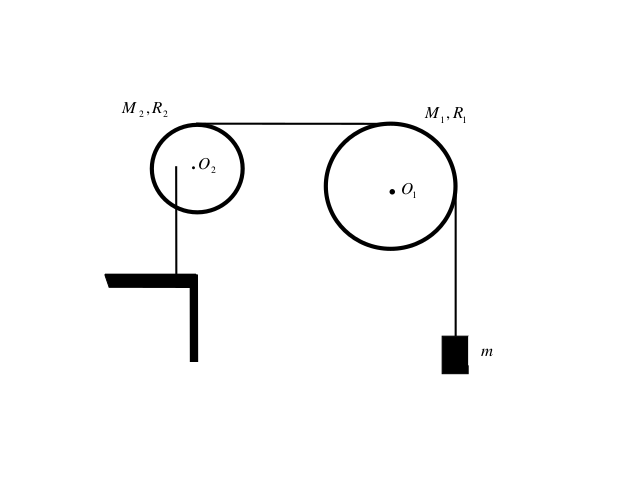
∆ύο τροχοί βρίσκονται με τα επίπεδά τους σε κατακόρυφη θέση και μπορούν να περιστρέφονται γύρω από σταθερούς οριζόντιους άξονες που διέρχονται από τα κέντρα τους \(O_1\) και \(O_2\) αντίστοιχα. Ο τροχός \(1\) έχει δύο αυλάκια στην περιφέρεια. Στο ένα είναι τυλιγμένο πολλές φορές νήμα στην άκρη του οποίου κρέμεται σώμα μάζας \(m\). Στο άλλο αυλάκι τυλίγεται νήμα το οποίο τον συνδέει με τον τροχό \(2\) καθώς τυλίγεται και στο δικό του αυλάκι. Σημείο της επιφάνειας του τροχού \(2\) και σε οριζόντια απόσταση \(r = \frac{R_2}{2}\) από το κέντρο \(O_2\) συνδέεται με κατακόρυφο νήμα σ’ ένα σταθερό βάθρο κι’ έτσι το σύστημα \(2\) ισορροπεί. Όλα τα νήματα είναι αβαρή και μη εκτατά. ∆ίνονται : \(M_1 = 6 Kg, R_1 = 0.2 m, M_2 = 2 Kg, R_2 = 0.1 m\) και \(m = 1 Kg\) Επίσης : \(g = 10 \frac{m}{s^2}\) και \(I_{cm} = \frac{1}{2} \cdot M \cdot R^2\)
Α. Να βρεθεί η τάση του κατακόρυφου νήματος που συνδέει τον τροχό \(2\) με το βάθρο.
Β. Κάποια στιγμή κόβουμε το νήμα, που συνδέει τον τροχό \(2\) με το βάθρο, οπότε το σύστημα μπαίνει σε κίνηση.
Β1. Να βρεθεί η επιτάχυνση καθόδου του σώματος μάζας \(m\).
Β2. Να βρεθεί η γωνιακή ταχύτητα περιστροφής του τροχού \(2\) όταν το σώμα μάζας \(m\) έχει κατέβει κατά \(y_1 = 4 m\).
Γ. Ας δεχθούμε τώρα ότι τη στιγμή που το σώμα κατέβηκε κατά \(y_1 = 4 m\), το νήμα που συνδέει τους δύο τροχούς έχει ξετυλιχτεί τελείως και επομένως ο τροχός \(2\) περιστρέφεται ελεύθερα . Να βρεθεί το ύψος καθόδου \(y_2\) του σώματος μάζας \(m\) από τη στιγμή που το νήμα ξετυλίχτηκε και μέχρις ότου ο τροχός \(2\) κάνει, ελεύθερα περιστρεφόμενος, \(N = \frac{20}{π}\) περιστροφές.
Απάντηση:
blog comments powered by Disqus