Συμπαγής κώνος
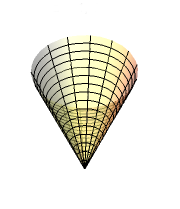
Στο σχήμα φαίνεται ένας αντεστραμμένος συμπαγής κώνος μάζας \(m = 10kg\), με ακτίνα βάσης \(r = 0.1m\), o οποίος μπορεί να στρέφεται χωρίς τριβές γύρω από νοητό κατακόρυφο άξονα που περνά από το κέντρο της βάσης του \(Ο\) και την κορυφή του \(Κ\). Στη βάση του κώνου έχουμε τυλίξει προσεκτικά ένα αβαρές και μη εκτατό νήμα, στο ελεύθερο άκρο του οποίου ασκούμε μία σταθερή οριζόντια δύναμη \(F\). Τη χρονική στιγμή \(t=0\), η γωνιακή ταχύτητα του κώνου έχει αλγεβρική τιμή
\[ω_ο = + 2 \frac{m}{s}\]ενώ τη χρονική στιγμή \(t_1 = 0.3s\), ο ρυθμός μεταβολής της κινητικής του ενέργειας είναι
\[\frac{dK}{dt} = 44 \frac{J}{s}\]Αν η ροπή της δύναμης \(F\) ως προς τον άξονα περιστροφής έχει την ίδια φορά με το διάνυσμα \(ω_ο\) να υπολογιστούν:
α) Η κινητική ενέργεια του κώνου την χρονική στιγμή \(t_1\).
β) Το έργο της δύναμης \(F\) από την χρονική στιγμή \(t=0\) μέχρι την χρονική στιγμή \(t_1\)
γ) Το πλήθος των στροφών που έχει κάμει μια ακτίνα του κύκλου της βάσης του κώνου από \(t = 0\) μέχρι την χρονική στιγμή \(t_1\).
δ) Το μέτρο της δύναμης \(F\)
ε) Το μέτρο της στροφορμής του κώνου την χρονική στιγμή που διπλασιάζεται η αρχική κινητική του ενέργεια.
Δίνεται ότι η ροπή αδράνειας του συμπαγούς κώνου ως προς τον άξονά του υπολογίζεται με την σχέση
\[I_{cm} = \frac{3}{10} \cdot m \cdot r^2\]όπου \(m\) η μάζα του κώνου και \(r\) η ακτίνα της βάσης του.
Απάντηση:
blog comments powered by Disqus