Μοριοδότηση 2023
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(β\)
Α2 - \(δ\)
Α3 - \(β\)
Α4 - \(α\)
Α5: \(Λ - Σ - Σ - Λ - Λ\)
Θέμα Β
Β1 - \((i)-2-6\)
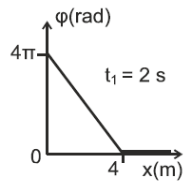
$t_1=2s, \quad x=0, \quad φ=4π rad: \quad 4π = 2π(\frac{2.1}{T}-\frac{0}{λ} ) \Rightarrow T=1s$
\[α) \underline {τρόπος}\]$t_1=2s, \quad x=4m, \quad φ=0: \quad 0= 2π(\frac{2.1}{1}-\frac{4}{λ} ) \Rightarrow λ=2m$
\[β) \underline {τρόπος}\] \[f=\frac{1}{T} \Rightarrow f=1Hz\] \[υ_δ=λ\cdot f \Rightarrow λ=2m\]Υπολογισμός του αριθμού των σημείων της χορδής που βρίσκονται σε ακραία θέση της τροχιάς τους.
\[α) \underline {τρόπος}\]$t_2=2.5s: \quad x_2=υ_δ\cdot t_2 \Rightarrow x_2=5m$
$y=A\cdot ημ2π(\frac{t}{T}-\frac{x}{λ} ) \Rightarrow y=A\cdot ημ(5π-πx) \quad (S.I.) \quad 0 \le x \le 5m$
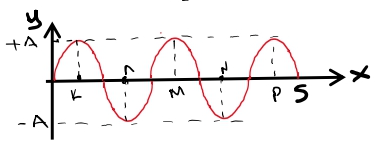
$t_2=2.5s=2\cdot T+\frac{T}{2} : \quad x_2=υ_δ\cdot t_2 \Rightarrow x_2=5m=2\cdotλ+\frac{λ}{2} $
Τα σημεία της χορδής που βρίσκονται σε ακραία θέση της τροχιάς τους είναι τα $Κ, Λ, Μ, Ν, Ρ$.
άρα σωστό το \(i\)
Β2 - \((ii)-2-6\)
Φωτοηλεκτρική εξίσωση του Einstein: \(K_{max}=h\cdot f - \phi\)
συχνότητα κατωφλίου $f_1: \quad 0=h\cdot f_1 - \phi \Rightarrow h\cdot f_1 = \phi \quad (1)$
$f_2=3f_1: \quad K_{max} = h\cdot 3f_1 - \phi \overset{(1)}{\implies} K_{max} = 3h\cdot f_1 - h\cdot f_1= 2h\cdot f_1 (2) $
\[Θ.Μ.Κ.Ε. \quad ΔΚ=ΣW \Rightarrow K_{τελ}-Κ_{αρχ}=W_{F_{ηλ}}\] \[Κ_{τελ}=0, \quad V_{αρχ}-V_{τελ}=V_0\] \[0-K_{max}=(-e)\cdot V_0 \overset{(2)}{\implies} -2h \cdot f_1=-e\cdot V_0 \Rightarrow V_0=\frac{2h \cdot f_1}{e}\]άρα σωστό το \(ii\)
Β3 - \(α(ii), β(i)-3-6\)
α) επιλογέας ταχυτήτων, Ευθύγραμμη ομαλή κίνηση, \(α=0 \Rightarrow ΣF=0\)
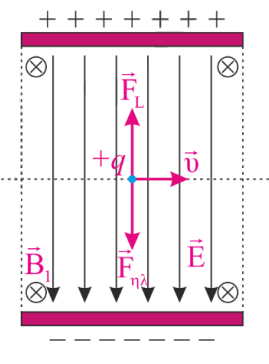
άρα σωστό το (ii)
β) Ομαλή κυκλική κίνηση σε μαγνητικό πεδίο $Β_2$.
\[R_1 = \frac{m_1 \cdot υ}{Β_2 \cdot q}, \quad R_2 = \frac{m_2 \cdot υ}{Β_2 \cdot q}\]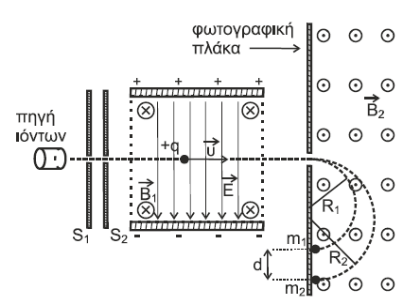
άρα σωστό το (i)
Θέμα Γ
Γ1-\((7)\)
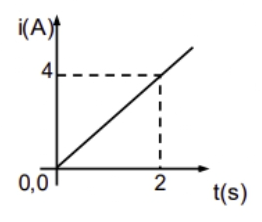
$0 \rightarrow 2s: q=[Εμβαδό]=\frac{β\cdot u}{2} \Rightarrow q=4C$
\[β) \underline {τρόπος}\] \[q = \displaystyle\int_0^{2} i dt = \int_0^{2} 2t dt = \Bigg[t^2 \Bigg]_0^2 = 4-0 = 4C\] \[γ) \underline {τρόπος}\]$2^{oς}$ κανόνας του Kirchhoff στο κύκλωμα $ΗΖΑΓH$
\[Ε_{επ} -i\cdot R -E_{αυτ} =0 \Rightarrow i = \frac{E_{επ}}{R} - \frac{E_{αυτ}}{R} \quad (1)\] \[Ε_{επ} = \frac{ΔΦ}{Δt} = \frac{B \cdot ΔS}{Δt} = \frac{B \cdot L \cdot Δx}{Δt} \quad(2)\] \[E_{αυτ} = L \cdot \frac{Δi}{Δt}\quad (3)\]Αντικαθιστούμε την $(2)$ και την $(3)$ στην εξίσωση $(1)$
\[i = \frac{B \cdot L \cdot Δx}{R \cdot Δt} - \frac{L}{R} \cdot \frac{Δi}{Δt} \Rightarrow i \cdot {Δt} = \frac{B \cdot L \cdot Δx}{R} - \frac{L}{R} \cdot Δi \quad (4)\] \[Δq = i \cdot Δt \quad (5)\] \[Δx = υ_0 \cdot Δt + \frac{1}{2} \cdot α \cdot Δt^2 \Rightarrow Δx = 6m \quad (6)\] \[Δi=i_{t=2} - i_{t=0} \Rightarrow Δi=4A \quad (7)\]Αντικαθιστούμε την $(5)$, την $(6)$ και την $(7)$ στην εξίσωση $(4)$
\[q = 6 - 2 = 4C\] \[δ) \underline {τρόπος}\]Η \(E_{αυτ}\) ΗΕΔ από αυτεπαγωγή είναι σταθερή.
\[E_{αυτ} = \frac{W}{q} \Rightarrow E_{αυτ} = \frac{ΔU_L}{q} \Rightarrow q= \frac{ΔU_L}{E_{αυτ}}\] \[ΔU_L = U_{L_{t=2}} - U_{L_{t=0}} = \frac{1}{2} \cdot L \cdot i^2-0 = 4J\] \[q= \frac{ΔU_L}{E_{αυτ}} = \frac{4J}{1V} \Rightarrow q= 4C\]Γ2-\((4)\)
H μεταλλική ράβδος $ΖΗ$ κινείται προς τα πάνω, οπότε αναπτύσεται $Ε_{επ}$ με πολικότητα όπως στο σχήμα. Το επαγωγικό ρεύμα έχει τέτοια φορά ώστε να αντιτίθεται στο αίτιο που το προκαλεί (κανόνας $Lenz$).
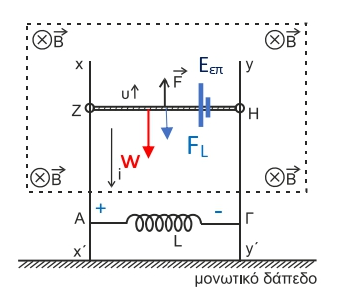
H ένταση του επαγωγικού ρεύματος αυξάνεται οπότε στο πηνίο αναπτύσεται $Ε_{αυτ}$ με πολικότητα όπως στο σχήμα, για τον ίδιο λόγο (κανόνας $Lenz$).
\[|E_{αυτ}| = |-L\cdot \frac{Δi}{Δt}| \Rightarrow |E_{αυτ}| = 1V\]Γ3-\((6)\)
$2^{oς}$ κανόνας του Kirchhoff στο κύκλωμα $ΗΖΑΓH$
\[Ε_{επ} -i\cdot R -E_{αυτ} =0 \Rightarrow B\cdot υ \cdot l = E_{αυτ} + i \cdot R \Rightarrow υ=1+2t \quad (S.I.)\]Ευθύγραμμη ομαλά επιταχυνόμενη κίνηση $υ=υ_0+αt, \quad υ_0=1 \frac{m}{s}, \quad α=2 \frac{m}{s^2}$
Γ4-\((8)\)
$t_1=2s$
\[ΣF=m \cdot α \Rightarrow F - F_L - m \cdot g = m \cdot α \Rightarrow F=10N\]$υ_1 = 1+2 \cdot 2 \Rightarrow υ_1=5\frac{m}{s}$
\[α) \underline {τρόπος}\] \[\frac{dW_F}{dt} = F \cdot \frac{dx}{dt} \cdot συνφ = F \cdot υ \Rightarrow \frac{dW_F}{dt}=50\frac{J}{s}\]$i_1 = 2 \cdot 2 \Rightarrow i_1 = 4A$
\[\frac{dU_L}{dt} = |E_{αυτ}| \cdot i_1 \Rightarrow \frac{dU_L}{dt} = 4 \frac{J}{s}\] \[β) \underline {τρόπος}\]Λόγω διατήρησης της ενέργειας θα πρέπει να ισχύει
\[P_F = P_W + P_{F_L} + \frac{dK}{dt}\] \[P_W = \frac{dW}{dt} = \frac{m\cdot g \cdot dx}{dt} = m\cdot g \cdot υ_1 = 25 \frac{J}{s}\] \[P_{F_L} = E_{επ} \cdot i_1 = B \cdot υ_1 \cdot L \cdot i_1 = 20 \frac{J}{s}\] \[\frac{dK}{dt} = ΣF \cdot υ_1 = (F - F_L - W) \cdot υ_1 = (F - Β \cdot i_1 \cdot L - m \cdot g) \cdot υ_1 = 5 \frac{J}{s}\]και αντικαθιστώντας στην αρχική εξίσωση $P_F = 50 \frac{J}{s}$.
\[P_{F_L} = \frac{dQ}{dt} + \frac{dU_L}{dt} \Rightarrow \frac{dU_L}{dt} = P_{F_L} - i_1^2 \cdot R \Rightarrow \frac{dU_L}{dt} = 4 \frac{J}{s}\]Θέμα Δ
Δ1-\((4)\)
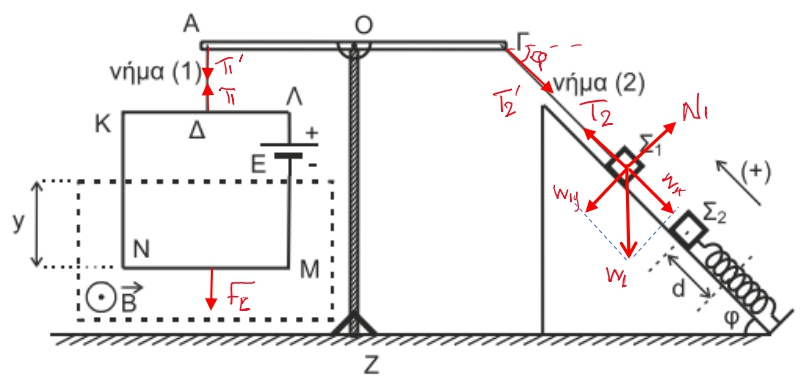
$m_1$, ισορροπία:
\[ΣF_x=0 \Rightarrow T_2 - m\cdot g \cdot ημφ =0 \Rightarrow T_2 = 18N\]$T_2=T’_2$ νήμα αβαρές μη εκτατό
ράβδος $ΑΓ$ ισορροπία:
\[Στ_Ο =0 \Rightarrow -T'_2 \cdot \frac{L}{2} \cdot ημφ + Τ_1 \cdot \frac{L}{2} = 0 \Rightarrow T_1 = 10.8N\]Δ2-\((4)\)
κύκλωμα $ΚΝΜΛ$ νόμος του Ohm $I=\frac{E}{R} \Rightarrow I=15A$
αβαρές πλαίσιο ισορροπία: $ΣF_y=0$ οι δυνάμεις Laplace αλληλοαναιρούνται.
\[ΣF_x = 0 \Rightarrow T_1 - F_L =0 \Rightarrow B \cdot I \cdot α = Τ_1 \Rightarrow B = 0.9T\]Δ3-\((7)\)
$m_2$ απλή αρμονική ταλάντωση:
\[Α = d = \frac{9π}{100} m, \quad D=k=m_2 \cdot ω^2 \Rightarrow ω=10 \frac{rad}{s}, \quad T=\frac{2π}{ω}= \frac{π}{5} s\]το $m_2$ στη θέση ισορροπίας της ταλάντωσής του
\[υ_2 = υ_{max} = A \cdot ω \Rightarrow υ_2 = \frac{9π}{10} \frac{m}{s}, \quad Δt = \frac{T}{4}= \frac{π}{20}s\]$m_1$ ευθύγραμμη ομαλά επιταχυνόμενη κίνηση με επιτάχυνση
\[α = \frac{ΣF}{m} = g \cdot ημφ \Rightarrow α =6 \frac{m}{s^2}\] \[υ_1 = υ_0 + α\cdot Δt \Rightarrow υ_1 = \frac{3π}{10} \frac{m}{s}\]$ΣF_{εξ} = 0 \Rightarrow $ μονωμένο σύστημα
\[Α.Δ.Ο. \quad \vec p_{τελ} = \vec p_{αρχ} \Rightarrow m_2 \cdot υ_2 - m_1 \cdot υ_1 = (m_1+m_2) \cdot V_k\]και μετά τις πράξεις $V_k=0$
Δ4-\((5)\)
συσσωμάτωμα $m_1+m_2$ απλή αρμονική ταλάντωση
\[D=k=(m_1+m_2) \cdot ω'^2 \Rightarrow ω'=5 \frac{rad}{s}\]θέση ισορροπίας $m_2$
\[ΣF_x = 0 \Rightarrow k\cdot Δl_2 = m_2 \cdot g \cdot ημφ \Rightarrow Δl_2 = 0.06m\]θέση ισορροπίας $m_1+m_2$
\[ΣF_x = 0 \Rightarrow k\cdot Δl_1 = (m_1+m_2) \cdot g \cdot ημφ \Rightarrow Δl_1 = 0.24m\] \[A'=Δl_1 - Δl_2 \Rightarrow Α'=0.18m\]αρχική φάση $φ_0$: $t=0: x=+A, υ=0$
\[x=A \cdot ημφ(ωt+φ_0) \Rightarrow ημφ_0 = +1 \Rightarrow φ_0=\frac{π}{2} rad\] \[x = 0.18 \cdot ημ(5t + \frac{π}{2} ) \quad (S.I.)\]Δ5-\((5)\)
\[α) \underline {τρόπος}\]συσσωμάτωμα $m_1+m_2$ απλή αρμονική ταλάντωση
\[F_{ελ} = k \cdot Δl \Rightarrow F_{ελ} = k \cdot (Δl_0-x) \Rightarrow F_{ελ} = 24 - 100\cdot x \quad (S.I.)\] \[β) \underline {τρόπος}\] \[ΣF = -D \cdot x \Rightarrow F_{ελ} - (m_1+m_2)\cdot g = -D \cdot x\] \[F_{ελ} = (m_1+m_2)\cdot g -k \cdot x \Rightarrow F_{ελ} = 24 - 100\cdot x \quad (S.I.)\]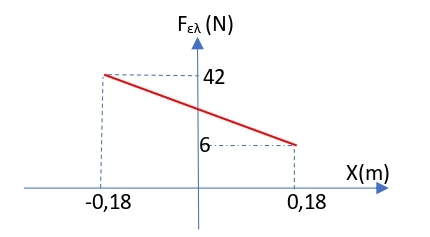
Μπορείτε να εκτυπώσετε τα θέματα και τις λύσεις σε μορφή pdf
blog comments powered by Disqus