Θέμα 2020
Θέμα Δ
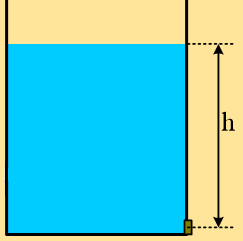
Η δεξαμενή του σχήματος έχει σχήμα κυλίνδρου με πυθμένα κύκλο ακτίνας \(R_1\) και κατακόρυφα τοιχώματα. Είναι τοποθετημένη στο έδαφος και περιέχει ιδανικό ρευστό μέχρι ύψος \(Η\). Στην πλευρική επιφάνεια της δεξαμενής σε επαφή με τον πυθμένα υπάρχει μικρή στρογγυλή οπή ακτίνας \(R_2\) από την οποία εκρέει το ρευστό. Να υπολογιστούν οι χρονικές συναρτήσεις του ύψους \(h(t)\) του ρευστού στη δεξαμενή και της παροχής \(Π(t)\) της οπής για την χρονική διάρκεια από την στιγμή που ανοίγει η οπή έως ότου αδειάσει η δεξαμενή.
Εξίσωση \(Bernulli\) από ένα σημείο \(Α\) της επιφάνειας του ρευστού έως ένα σημείο \(Β\) στην οπή.
\[P_A + \frac{1}{2} \cdot ρ \cdot υ_Α^2 + ρ \cdot g \cdot h = P_B + \frac{1}{2} \cdot ρ \cdot υ_B^2\]Για τις ακτίνες ισχύει \(R_1 >> R_2\) οπότε βγάζουμε το συμπέρασμα ότι \(υ_Α << υ_Β\) και αγνοούμε έτσι την ταχύτητα \(υ_Α\). Για τις πιέσεις ισχύει \(P_A = P_B = P_{ατμ}\) οπότε η εξίσωση \(Bernulli\) γίνεται:
\[ρ \cdot g \cdot h = \frac{1}{2} \cdot ρ \cdot υ_B^2 \Rightarrow υ_Β = \sqrt{2 \cdot g \cdot h}\]Η παροχή ορίζεται ως ο ρυθμός μεταβολής του όγκου του ρευστού που εκκρέει.
\[Π = \frac{dV}{dt} \Rightarrow Π = \frac{d(V_{ολ} - V_{υγρού}) }{dt} \Rightarrow Π = - π \cdot R_1^2 \frac{dh}{dt}\]και δίνεται από την σχέση
\[Π = Α \cdot υ_B \Rightarrow Π = π \cdot R_2^2 \cdot υ_B \Rightarrow Π = π \cdot R_2^2 \cdot \sqrt{2 \cdot g \cdot h}\]Από τις δυο προηγούμενες σχέσεις
\[π \cdot R_2^2 \cdot \sqrt{2 \cdot g \cdot h} = \frac{ΔV}{Δt} \Rightarrow π \cdot R_2^2 \cdot \sqrt{2 \cdot g \cdot h} = -π \cdot R_1^2 \cdot \frac{dh}{dt}\]απλοποιούμε το \(π\) και υψώνουμε στο τετράγωνο, οπότε
\[\frac{h'}{\sqrt{h}} = -(\frac{R_2}{R_1})^2 \cdot \sqrt{2 \cdot g} \Rightarrow \frac{h'}{2\sqrt{h}} = -(\frac{R_2}{R_1})^2 \cdot \sqrt{\frac{g}{2}}\]και μετά τις πράξεις
\[(\sqrt{h(t)})' = - (\frac{R_2}{R_1})^2 \cdot \sqrt{\frac{g}{2} } \Rightarrow \sqrt{h(t)} = - (\frac{R_2}{R_1})^2 \cdot \sqrt{\frac{g}{2} } \cdot t +c \Rightarrow h(t) = (- (\frac{R_2}{R_1})^2 \cdot \sqrt{\frac{g}{2} } \cdot t +c)^2\]όπου η σταθερά \(c\) υπολογίζεται από τις αρχικές συνθήκες για τις οποίες θα έχουμε την χρονική στιγμή \(t=0 \quad\) το ύψος είναι \(h(t) = H\) οπότε \(c = H\) και η τελική συνάρτηση είναι:
\[h(t) = (H - (\frac{R_2}{R_1})^2 \cdot \sqrt{\frac{g}{2} } \cdot t)^2\]Ενώ η τελική συνάρτηση για την παροχή μετά τις πράξεις είναι:
\[Π(t) = π \cdot R_2^2 \cdot H \cdot \sqrt{2g} - \frac{π \cdot R_2^4 \cdot g }{R_1^2} \cdot t\]Θέμα Γ
Δύο κατακόρυφοι μεταλλικοί αγωγοί \(Αy_1\) και \(Γy_2\), αμελητέας ωμικής αντίστασης, συνδέονται μεταξύ τους στα σημεία \(Α\) και \(Γ\) μέσω ωμικής αντίστασης \(R_2 = 3Ω\). Παράλληλα με την ωμική αντίσταση συνδέεται πηγή ΗΕΔ \(Ε=10Volt\) και εσωτερικής αντίστασης \(r=1Ω\). Οριζόντιος αγωγός \(ΚΛ\) έχει την δυνατότητα να μετακινείται πάνω στους μεταλλικούς αγωγούς χωρίς τριβές. Ο οριζόντιος αγωγός έχει μάζα \(m_1=4 kg\), μήκος \(l=50cm\), ωμική αντίσταση \(R_1=1.5Ω\) και είναι δεμένος στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \(k = 100 \frac{N}{m}\) το πάνω άκρο του οποίου είναι ακλόνητα στερεωμένο, όπως φαίνεται στο σχήμα.
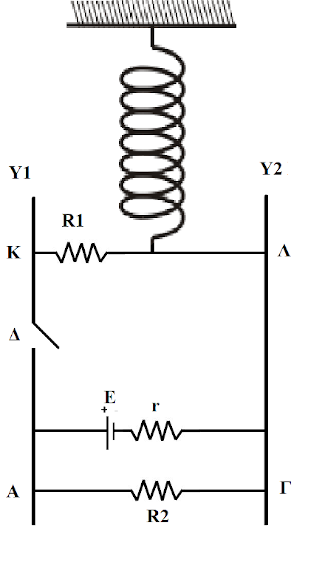
Όλο το σύστημα των κατακόρυφων αγωγών, της πηγής, των αντιστατών και του ελατηρίου βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο. Όταν ο διακόπτης \(Δ\) είναι κλειστός ο αγωγός \(ΚΛ\) ισορροπεί ακίνητος, έτσι ώστε η επιμήκυνση του ελατηρίου να είναι \(Δl_1 = 0.5m\).
1) Να σχεδιαστεί η φορά και να υπολογιστεί το μέτρο της έντασης του ομογενούς μαγνητικού πεδίου.
Την χρονική στιγμή \(t=0\) ανοίγουμε τον διακόπτη \(Δ\) οπότε ο αγωγός \(ΚΛ\) εκτελεί απλή αρμονική ταλάντωση. Θεωρήστε θετική φορά την αρχική φορά κίνησης του αγωγού.
2) Να γραφεί η σχέση που δίνει την απομάκρυνση του αγωγού \(ΚΛ\) από την θέση ισορροπίας του, σαν συνάρτηση του χρόνου και να γίνει η γραφική της παράσταση για την χρονική διάρκεια μιας περιόδου.
3) Να υπολογιστεί η ηλεκτρεγερτική δύναμη από επαγωγή που αναπτύσσεται στα άκρα του αγωγού \(ΚΛ\) καθώς αυτός ταλαντώνεται στο κατακόρυφο επίπεδο κάθετα στις δυναμικές γραμμές του οριζόντιου μαγνητικού πεδίου σαν συνάρτηση του χρόνου.
Την χρονική στιγμή που μηδενίζεται για πρώτη φορά ο ρυθμός μεταβολής της επαγωγικής τάσης που αναπτύσσεται στα άκρα του αγωγού \(ΚΛ\), βλήμα μάζας \(m_2 = 1kg\) κινούμενο με ταχύτητα \(υ_2 = 0.5 \frac{m}{s}\) στην κατακόρυφη διεύθυνση του ελατηρίου και με φορά προς τα κάτω, σφηνώνεται ακαριαία στο κέντρο μάζας του αγωγού \(ΚΛ\). Το συσσωμάτωμα που προκύπτει από την σύγκρουση εκτελεί απλή αρμονική ταλάντωση.
4) Να υπολογιστεί η ταχύτητα του συσσωματώματος αμέσως μετά την κρούση και το διάστημα που θα διανύσει αυτό μέχρι να σταματήσει στιγμιαία για δεύτερη φορά.
5) Να υπολογιστεί ο ρυθμός μεταβολής της κινητικής ενέργειας του συσσωματώματος όταν για πρώτη φορά αυτό διέρχεται από την αρχική θέση ισορροπίας του αγωγού \(ΚΛ\) (όπου η επιμήκυνση του ελατηρίου είναι \(Δl_1 = 0.5m\)).
Θέμα Β
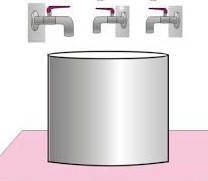
Οι τρεις βρύσες Α, Β και Γ, σταθερής παροχής χρησιμοποιούνται για να γεμίσουν το άδειο δοχείο με νερό. Όταν οι βρύσες \(Α\) και \(Β\) είναι ανοικτές, το δοχείο γεμίζει σε \(2 min\). Όταν οι βρύσες \(Β\) και \(Γ\) είναι ανοικτές, το δοχείο γεμίζει σε \(3min\). Όταν οι βρύσες \(Α\) και \(Γ\) είναι ανοικτές, το δοχείο γεμίζει σε \(4min\). Όταν είναι ανοικτές και οι τρεις βρύσες, το δοχείο γεμίζει σε χρόνο:
- $$ \frac{24}{13} min $$
- $$ \frac{13}{24} min $$
- $$ \frac{1}{2} min $$
- $$ 9 min $$
Επιλέξτε και δικαιολογήστε!
Θέμα Α
Δύο ίδια δοχεία έχουν στα πλευρικά τοιχώματά τους οπές ίδιου εμβαδού διατομής σε σημεία πολύ κοντά στον πυθμένα. Θεωρούμε ότι η διατομή κάθε οπής είναι πολύ μικρότερη από την διατομή της ελεύθερης επιφάνειας του υγρού και ότι η πίεση γύρω από τα δοχεία είναι ίση με την ατμοσφαιρική. Τα δοχεία γεμίζουν με υγρά διαφορετικής πυκνότητας για τα οποία ισχύει \(ρ_1 > ρ_2\). Η ολική πίεση κοντά στον πυθμένα είναι το άθροισμα της υδροστατικής και της ατμοσφαιρικής. Εάν ανοίξουμε τις οπές ταυτόχρονα:
1) το δοχείο \(1\) θα αδειάσει σε μικρότερο χρόνο γιατί η εσωτερική πίεση κοντά στην οπή είναι μεγαλύτερη
2) τα δοχεία θα αδειάσουν στον ίδιο χρόνο
3) το δοχείο \(2\) θα αδειάσει σε μικρότερο χρόνο διότι η ολική πίεση κοντά στον πυθμένα όταν είναι ανοιχτή η οπή δεν είναι ίση με το άθροισμα της υδροστατικής και της ατμοσφαιρικής πίεσης
4) δεν μπορούμε να γνωρίζουμε ποιο δοχείο θα αδειάσει πρώτα
blog comments powered by Disqus