Προσομοίωση 2018

ΘΕΜΑ Α

$Α_1$ Σε κάθε μετωπική κρούση μεταξύ δύο σωμάτων διατηρείται

η ορμή κάθε σώματος ξεχωριστά
η κινητική ενέργεια κάθε σώματος ξεχωριστά
η κινητική ενέργεια του συστήματος των δύο σωμάτων
η ορμή του συστήματος των δύο σωμάτων

(Μονάδες 5)

$Α_2$ Σε ένα γραμμικό ελαστικό μέσο διαδίδονται ταυτόχρονα δύο κύματα με ίδιο πλάτος, ίδια συχνότητα και αντίθετες ταχύτητες. Δύο σημεία $Μ$ και $Ν$ βρίσκονται εκατέρωθεν ενός σημείου $Λ$ που παραμένει συνεχώς ακίνητο. Τα σημεία απέχουν αποστάσεις $\frac{λ}{3}$ και $\frac{2λ}{3}$ αντίστοιχα από το $Λ$. Οι ταλαντώσεις των σημείων $Μ$ και $Ν$ έχουν διαφορά φάσης:

$$Δφ = 0$$
$$Δφ = π$$
$$Δφ = \frac{π}{3}$$
$$Δφ = \frac{2π}{3}$$

(Μονάδες 5)

$Α_3$ Σώμα μάζας $m$ είναι δεμένο στο ελεύθερο άκρο οριζόντιου ελατηρίου σταθεράς $k$ και εκτελεί απλή αρμονική ταλάντωση σε λείο οριζόντιο επίπεδο με περίοδο $Τ$ και πλάτος $Α$. Αντικαθιστούμε το σώμα μάζας $m$ με άλλο σώμα τετραπλάσιας μάζας και το αναγκάζουμε και πάλι να εκτελέσει απλή αρμονική ταλάντωση πλάτους $Α$. Τότε

η περίοδος της ταλάντωσης τετραπλασιάζεται
η ολική ενέργεια της ταλάντωσης διπλασιάζεται
η μέγιστη ταχύτητα της ταλάντωσης υποδιπλασιάζεται
η σταθερά επαναφοράς της ταλάντωσης τετραπλασιάζεται

(Μονάδες 5)

$Α_4$ Σε κάθε πλαστική κρούση μεταξύ δύο σωμάτων

διατηρείται η κινητική ενέργεια του συστήματός τους
που πριν την κρούση τα σώματα έχουν αντίθετες ορμές, το δημιουργούμενο συσσωμάτωμα παραμένει ακίνητο
το σώμα μικρότερης μάζας υφίσταται μικρότερη κατά μέτρο μεταβολή στην ορμή του
που πριν την κρούση τα σώματα κινούνται σε αντίθετες κατευθύνσεις με ίσες κινητικές ενέργειες, η αρχική κινητική ενέργεια του συστήματος μετατρέπεται πάντα σε θερμότητα

(Μονάδες 5)

$Α_5$ Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.

Ένας ταλαντωτής εκτελεί φθίνουσα ταλάντωση. Η δύναμη που αντιστέκεται στην κίνηση έχει τη μορφή: $$F΄=–b \cdot υ$$ Ο λόγος δύο διαδοχικών μέγιστων απομακρύνσεων προς την ίδια κατεύθυνση παραμένει σταθερός
Το σύστημα ανάρτησης του αυτοκινήτου είναι μια περίπτωση δημιουργίας εξαναγκασμένων ταλαντώσεων
Ένα σώμα εκτελεί κίνηση που προέρχεται από την σύνθεση των εξής απλών αρμονικών ταλαντώσεων $$y_1 = 0.1 \cdot ημ10t \ (SI) \qquad y_2 = 0.2 \cdot ημ(10t+\pi) \ (SI)$$ Αν οι δυο ταλαντώσεις εξελίσονται στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας τότε η φάση της σύνθετης ταλάντωσης είναι $$φ = 10t + \pi \ (SI)$$
Σε μια κρούση αμελητέας χρονικής διάρκειας η δυναμική ενέργεια των σωμάτων, που εξαρτάται από τη θέση τους στο χώρο, δεν μεταβάλλεται
Σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις, ίδιου πλάτους Α, ίδιας διεύθυνσης και μηδενικής αρχικής φάσης, γύρω από την ίδια θέση ισορροπίας. Αν οι δύο ταλαντώσεις έχουν συχνότητες οι οποίες διαφέρουν λίγο μεταξύ τους τότε η συνισταμένη ταλάντωση του συστήματος είναι απλή αρμονική

(Μονάδες 5)

ΘΕΜΑ Β

$Β_1$ Δύο εγκάρσια αρμονικά κύματα παράγονται από σύγχρονες πηγές $Π_1$ και $Π_2$ που αρχίζουν να ταλαντώνονται τη χρονική στιγμή $t=0$ με εξίσωση $y = 0.5 ημ4πt \ (S.I)$ και διαδίδονται στην επιφάνεια υγρού που ηρεμεί. Τα κύματα συμβάλλουν σε σημείο $Σ$. Το μέτρο της μέγιστης ταχύτητας ταλάντωσης του σημείου $Σ$ μεταβάλλεται σε συνάρτηση με τον χρόνο όπως στο διάγραμμα του παρακάτω σχήματος.

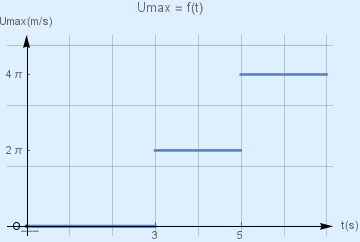
σχήμα

Αν $r_1$ και $r_2$ οι αποστάσεις του σημείου $Σ$ από τις πηγές $Π_1$ και $Π_2$ αντίστοιχα με $r_1 > r_2$ και $λ$ το μήκος κύματος των κυμάτων τότε:

$$r_1 - r_2 = λ$$
$$r_1 - r_2 = 2λ$$
$$r_1 - r_2 = 4λ$$

Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

(Μονάδες 9)

$Β_2$ Δύο σώματα $Σ_1$, $Σ_2$ με μάζες $m_1 = m$ και $m_2 = m$, κινούνται πάνω σε λείο οριζόντιο επίπεδο σε κάθετες μεταξύ τους διευθύνσεις και με ταχύτητες μέτρου $υ_1 = υ$ και $υ_2 = 3υ$ αντίστοιχα. Κάποια χρονική στιγμή τα σώματα συγκρούονται πλαστικά. Τα ποσά θερμότητας που ελευθερώνονται κατά την κρούση είναι:

$$\frac{5}{2} \cdot m \cdot υ^2$$
$$\frac{3}{2} \cdot m \cdot υ^2$$
$$\frac{1}{2} \cdot m \cdot υ^2$$

Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

(Μονάδες 8)

$Β_3$ Δύο σώματα $Σ_1$ και $Σ_2$ με μάζες $3m$ και $m$ αντίστοιχα, είναι τοποθετημένα σε λείο οριζόντιο επίπεδο και είναι δεμένα μεταξύ τους με νήμα αβαρές και μη εκτατό, μήκους $l$. To $Σ_2$ είναι δεμένο στην άκρη οριζόντιου ελατηρίου σταθεράς $k$. Στο $Σ_1$ ασκείται σταθερή οριζόντια δύναμη $F$ με αποτέλεσμα το σύστημα των σωμάτων να ισορροπεί ακίνητο, όπως φαίνεται στο σχήμα. Την χρονική στιγμή $t=0$ παύει να ασκείται η οριζόντια δύναμη $F$. Αν γνωρίζετε ότι τα σώματα συγκρούονται στην θέση του φυσικού μήκους του ελατηρίου και ότι το σώμα $Σ_2$ την στιγμή της σύγκρουσης διέρχεται από αυτή την θέση για δεύτερη φορά, τότε το μήκος του νήματος δίνεται από τον τύπο:

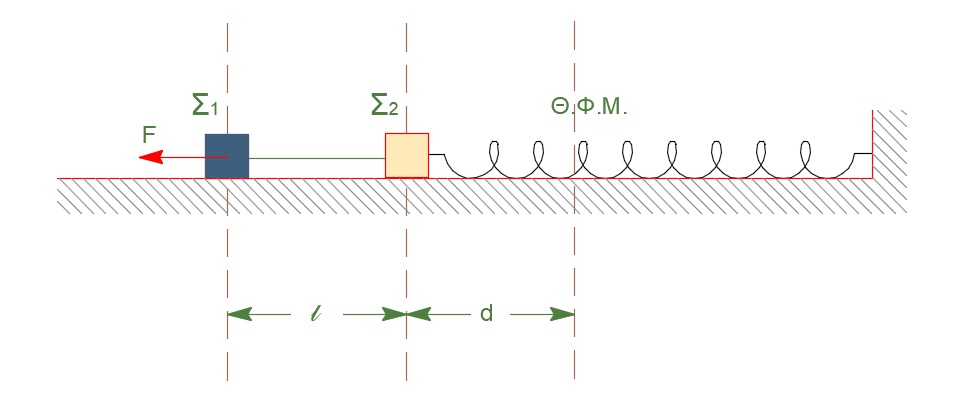
σχήμα

$$l = \frac{πF}{k}$$
$$l = \frac{πF}{2k}$$
$$l = \frac{πF}{4k}$$

Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

(Μονάδες 8)

ΘΕΜΑ Γ

Μια ελαστική ομογενείς χορδή ΟΓ μήκους $L = 120 cm$ στερεώνεται με τη βοήθεια ενός μικρού δακτυλιδιού $Δ$ σε κατακόρυφη λεπτή ράβδο $ΖΖ’$, όπως δείχνει το σχήμα. Το δακτυλίδι $Δ$ είναι ελεύθερο να κινείται κατά μήκος της λεπτής ράβδου χωρίς τριβές. Το άκρο $Ο$ τίθεται σε ταλάντωση, με τη βοήθεια μηχανικού ταλαντωτή, τη χρονική στιγμή $t = 0$, με φορά προς τα πάνω την οποία θεωρούμε θετική. Δημιουργείται έτσι ένα εγκάρσιο κύμα πλάτους $5 cm$ που διαδίδεται από αριστερά προς δεξιά κατά μήκος της χορδής με ταχύτητα $υ = 1 \frac{m}{s}$

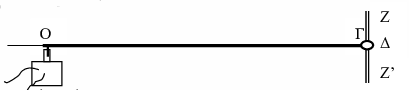
σχήμα

Δύο σημεία της χορδής $Μ$ και $Ν$ απέχουν από το $Ο$ απόσταση $20 cm$ και $80 cm$ αντίστοιχα. Το τρέχον κύμα φτάνει στα δύο σημεία με διαφορά φάσης $3π \ rad$.

$Γ_1$ Να βρεθεί η εξίσωση του τρέχοντος κύματος που διαδίδεται κατά μήκος της χορδής, λαμβάνοντας το σημείο $Ο$ ως αρχή $(x = 0)$ και τη φορά προς τα δεξιά θετική.

(Μονάδες 4)

$Γ_2$ Να βρεθεί, τη χρονική στιγμή $t_1 = 1 s$ η ταχύτητα και η επιτάχυνση του σημείου $Ν$.

(Μονάδες 4)

$Γ_3$ Να γράψετε την εξίσωση της φάσης των σημείων της χορδής σε συνάρτηση με την απόσταση $x$ από την πηγή κατά τη χρονική στιγμή $t_2 = 1.1 s$ και να χαράξετε τη γραφική της παράσταση.

(Μονάδες 5)

$Γ_4$ Να σχεδιάσετε, το στιγμιότυπο του κύματος την χρονική στιγμή $t_2 = 1.1 s$.

(Μονάδες 6)

Το κύμα από την πηγή $Ο$ ανακλάται χωρίς να εισάγει διαφορά φάσης, στο σημείο $Γ$ και το ανακλώμενο κύμα διαδιδόμενο προς αριστερά συμβάλλει με το αρχικό κύμα. Ως αποτέλεσμα της συμβολής είναι η δημιουργία ενός στάσιμου κύματος με το σημείο $Ο$ να είναι κοιλία.

$Γ_5$ Να γράψετε την εξίσωση της ταχύτητας ταλάντωσης των σημείων της χορδής σε συνάρτηση με την απόσταση $x$ από την πηγή κατά τη χρονική στιγμή $t_3 = 2.65 s$ και να χαράξετε τη γραφική της παράσταση.

(Μονάδες 6)

ΘΕΜΑ Δ

Τα σώματα $Σ_1$ και $Σ_2$ του παρακάτω σχήματος έχουν μάζες $m_1=4kg$ και $m_2=2kg$ αντίστοιχα. Το κάτω μέρος του σώματος $Σ_1$ έχει ενσωματωμένη αβαρή πηγή ηχητικών κυμάτων συχνότητας $f_s = 680 Hz$ και πάνω στο σώμα $Σ_2$ υπάρχει ακίνητος ανιχνευτής κυμάτων. Το κατακόρυφο ιδανικό ελατήριο σταθεράς $k=100 \frac{N}{m}$ το οποίο έχει το φυσικό του μήκος $l_o$ (δηλαδή δεν είναι παραμορφωμένο) είναι προσαρτημένο στο σώμα $Σ_1$ και η διάταξη συγκρατείται ακίνητη έτσι ώστε το ελεύθερο άκρο του ελατηρίου να βρίσκεται σε ύψος $h= 60cm$ πάνω από το σώμα $Σ_2$ το οποίο είναι ακίνητο πάνω σε οριζόντιο δάπεδο. Το σώμα $Σ_1$ με το ελατήριο αφήνεται ελεύθερο να κινηθεί κατακόρυφα και την $t=0$ το ελεύθερο άκρο του ελατηρίου καρφώνεται ακλόνητα και ακαριαία στο $Σ_2$ χωρίς απώλεια ενέργειας και χωρίς το σώμα $Σ_2$ να αναπηδήσει. Στη συνέχεια το σώμα $Σ_1$ ξεκινά να εκτελεί Απλή Αρμονική Ταλάντωση σταθεράς $D = k$. Η αντίσταση του αέρα θεωρείται αμελητέα και το μέτρο της επιτάχυνσης της βαρύτητας είναι $g=10 \frac{m}{s^2}$. Το ελατήριο έχει αρκετά μεγάλο μήκος ώστε το $Σ_1$ να μην έλθει ποτέ σε επαφή με το $Σ_2$

$Δ_1$ Να υπολογίσετε το μέτρο της ταχύτητας $υ_1$ του σώματος $Σ_1$ τη χρονική στιγμή που το ελεύθερο άκρο του ελατηρίου καρφώνεται στο $Σ_2$ και την περίοδο $Τ$ της απλής αρμονικής ταλάντωσης που εκτελεί το σώμα $Σ_1$

(Μονάδες 4)

$Δ_2$ Θεωρώντας θετική φορά την προς τα πάνω να γράψετε την εξίσωση της απομάκρυνσης του $Σ_1$ από την θέση ισορροπίας του σαν συνάρτηση του χρόνου για όσο χρόνο το $Σ_2$ είναι σε επαφή με το δάπεδο.

(Μονάδες 6)

$Δ_3$ Να υπολογίσετε το μέγιστο και το ελάχιστο μήκος κύματος που καταγράφει ο ανιχνευτής κυμάτων εάν δίνεται η ταχύτητα διάδοσης του ήχου στον ακίνητο αέρα $υ_{ηχ} = 340 \frac{m}{s}$

(Μονάδες 7)

$Δ_4$ Να αποδείξετε ότι το $Σ_2$ χάνει την επαφή του με το δάπεδο κάποια χρονική στιγμή $t$ και να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας του $Σ_1$ τη χρονική στιγμή $t$.

(Μονάδες 8)

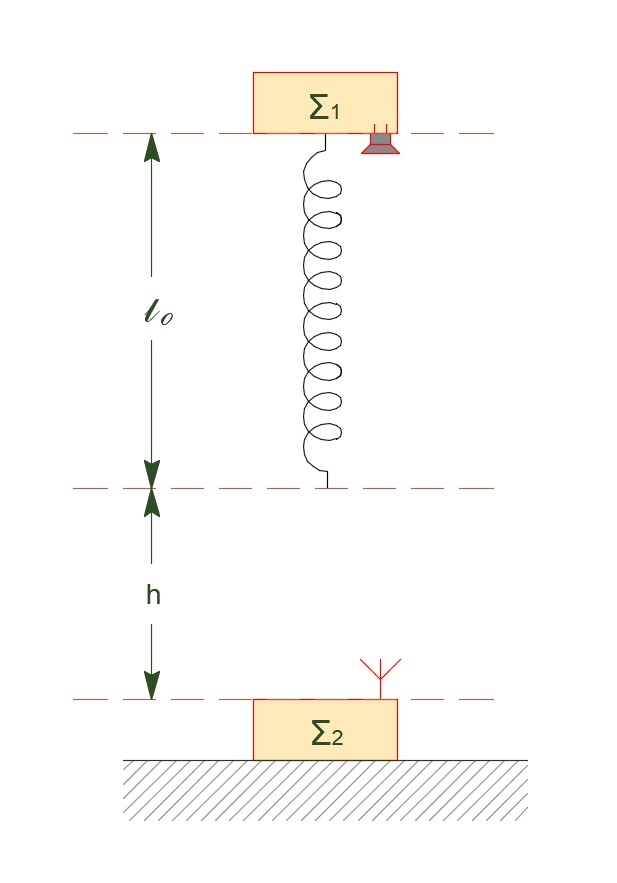
σχήμα

Να θεωρήσετε αμελητέες τις διαστάσεις των σωμάτων.

Επιμέλεια θεμάτων: Μπόγδανος Αθανάσιος, Πετρίδης Παναγιώτης

Ενδεικτικές απαντήσεις

Θέμα Α

Α1 - $δ$

Α2 - $α$

Α3 - $γ$

Α4 - $β$

Α5: $Σ - Λ - Σ - Σ - Λ$

Θέμα Β

B1-$(γ)$

σχήμα

\[Π_1 Π_2 \qquad y = 0.5 ημ 4πt \qquad S.I.\] \[ω = 4π \frac{rad}{s}, Τ = \frac{2π}{ω} = 0.5 s\] \[r_1 > r_2 \Rightarrow t_1 > t_2\] \[t_1 = \frac{r_1}{υ_δ} = 5 sec \Rightarrow r_1 = 5 \cdot \frac{λ}{Τ} = 10 \cdot λ\] \[t_2 = \frac{r_2}{υ_δ} = 3 sec \Rightarrow r_2 = 3 \cdot \frac{λ}{Τ} = 6 \cdot λ\] \[r_1 - r_2 = 4λ \qquad (γ)\]

B2-$(α)$

\[p_1 = m_1 \cdot υ_1 = m \cdot υ\] \[p_2 = m_2 \cdot υ_2 = 3m \cdot υ\] \[p_τ = (m_1 + m_2) \cdot V_k = 4m \cdot V_k\] \[Α.Δ.Ο. \qquad \vec{p}_{αρχ} = \vec{p}_{τελ} \Rightarrow p_τ ^2 = p_1 ^2 + p_2 ^2 \Rightarrow V_k ^2 = \frac{5}{2} υ^2\] \[Κ_{αρχ} = \frac{1}{2} m_1 υ_1^2 + \frac{1}{2} m_2 υ_2^2 = 5 m υ^2\] \[Κ_{τελ} = \frac{1}{2} (m_1 + m_2) V_k^2 = \frac{5}{2} m υ^2\] \[Q_{θερ} = Κ_{αρχ} - Κ_{τελ} = \frac{5}{2} m υ^2 \qquad (α)\]

B3-$(β)$

σχήμα

Το νήμα είναι αβαρές και μη εκτατό. Τα σώματα $m_1$ και $m_2$ αρχικά ισοορροπούν. Στο σώμα $m_1$ ασκείται η δύναμη $F$ και η τάση του νήματος, ενώ στο σώμα $m_2$ ασκείται η τάση του νήματος (ίδιο μέτρο) και η δύναμη του ελατηρίου. Άρα ισχύει τελικά

\[F = k \cdot d\]

Το σύστημα των σωμάτων $m_1$ και $m_2$ εκτελεί απλή αρμονική ταλάντωση κινούμενο από την ακραία θέση του ($A = d$) έως την θέση ισορροπίας του που είναι και θέση του φυσικού μήκους του ελατηρίου.

\[D = k = (m_1 + m_2) ω^2 \Rightarrow ω = \sqrt \frac{k}{4m}\]

Η μέγιστη ταχύτητα για κάθε σώμα δίνεται από την σχέση

\[υ_{max} = ω \cdot A = \sqrt \frac{k}{4m} \cdot A\]

Σε χρόνο $Δt = \frac{T}{4}$ το σύστημα των δύο σωμάτων φτάνει στην θέση του φυσικού μήκους του ελατηρίου. Στη συνέχεια το σώμα μάζας $m_2$ λόγω της δύναμης του ελατηρίου επιβραδύνεται, ενώ το σώμα μάζας $m_1$ κινείται με ταχύτητα $υ_{max}$ κάνοντας ευθύγραμμη ομαλή κίνηση, άρα το νήμα χαλαρώνει. To σώμα μάζας $m_2$ εκτελεί απλή αρμονική ταλάντωση για την οποία ισχύει:

\[D = k = m_2 \cdot ω^2 \Rightarrow ω = \sqrt \frac{k}{m} \Rightarrow T_2 = 2π \sqrt \frac{m}{k}\]

Σε χρόνο $Δt' = \frac{T_2}{2}$ το σώμα μάζας $m_2$ περνά ξανά από την θέση φυσικού μήκους που είναι και θέση ισορροπίας της ταλάντωσης, ενώ την ίδια χρονική στιγμή το σώμα μάζας $m_1$ που εκτελεί ευθύγραμμη ομαλή κίνηση βρίσκεται και αυτό στην ίδια θέση και έχει διανύσει απόσταση:

\[l = υ_{max} \cdot \frac{T_2}{2} = \sqrt \frac{k}{4m} \cdot d \cdot \frac{1}{2} \cdot 2π \sqrt \frac{m}{k} = \frac{π \cdot d}{2}\]

Τέλος κάνοντας την αντικατάσταση $d = \frac{F}{k}$ έχουμε:

\[F = \frac{π \cdot F}{2k} \qquad (β)\]

Θέμα Γ

Γ1

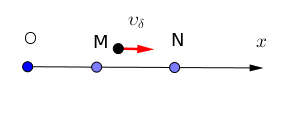
σχήμα

\[y_o = A \cdot ημωt \qquad y = A \cdot ημ ( \frac{2πt}{T} - \frac{2πx}{λ})\] \[φ_Μ - φ_Ν = \frac{2πt}{T} - \frac{2πx_Μ}{λ} - (\frac{2πt}{T} - \frac{2πx_Ν}{λ}) \Rightarrow 3π = 2π \frac{x_N-x_M}{λ} \Rightarrow λ = 0.4m\] \[υ_δ = \frac{λ}{Τ} \Rightarrow T = 0.4s \qquad ω = \frac{2π}{Τ} \Rightarrow ω = 5π \frac{rad}{s}\] \[y = 0.05 \cdot ημ(5πt - 5πx) \qquad S.I.\]

Γ2

\[t_1 = 1 sec \qquad x_1 = υ_δ \cdot t_1 = 1.0m > 0.8m = x_N\] \[υ_Ν = 5π \cdot 0.05 \cdot συν(5π - 5π \cdot 0.8) = -\frac{π}{4} \frac{m}{s}\] \[α_Ν = - 25π^2 \cdot 0.05 \cdot ημ(5π - 5π \cdot 0.8) = 0\]

Γ3

\[t_2 = 1.1 sec \qquad x_2 = υ_δ \cdot t_2 = 1.1m\] \[φ=\begin{cases} 5.5π - 5πx, & 0\le x\le 1.1m \\\ δεν \qquad ορίζεται, & 1.1m < x \end{cases}\] \[x=0 \qquad φ = 5.5 rad\] \[x=1.1m \qquad φ = 0 rad\]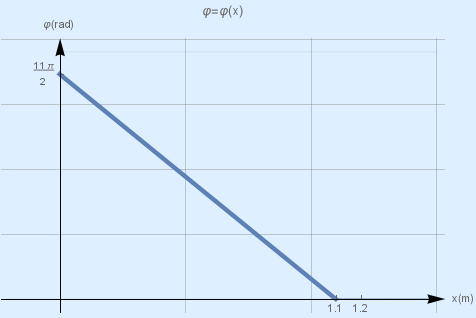

σχήμα

Γ4

\[t_2 = 1.1s \qquad x_2 = υ_δ t_2 = 1.1m \qquad N_2 = \frac{x_2}{λ} = 2.75 μ.κ.\] \[y=\begin{cases} 0.05 \cdot ημ(5.5π - 5πx), & 0\le x\le 1.1m \\\ 0, & 1.1m < x \le 1.2m \end{cases}\] \[x = 0 \qquad y = -0.05m\] \[x = 0.1m \qquad y = 0\]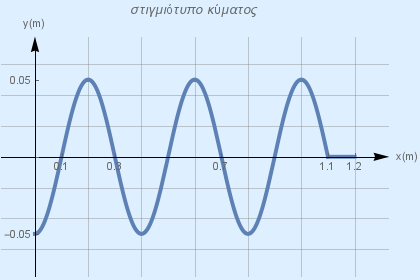

σχήμα

Γ5

Για το στάσιμο κύμα ισχύει:

\[y = y_1 + y_2 = 2A συν\frac{2πx}{λ} \cdot ημ\frac{2πt}{T} \Rightarrow y = 0.1 \cdot συν 5πx \cdot ημ 5πt \qquad S.I.\] \[t_3 = 2.65s\] \[υ = 5π \cdot 0.1 \cdot συν 5πx \cdot συν 5πt \qquad S.I.\] \[υ = \frac{π}{2} \cdot συν 5πx \cdot συν (5π \cdot 2.65) \qquad συν13.25π = συν(6π+π+\frac{π}{4}) = - \frac{\sqrt{2}}{2})\] \[υ = - \frac{π \sqrt2}{4} συν 5πx \qquad S.I. \qquad 0 \le x \le 1.2m\] \[x = 0 \qquad υ = - \frac{π \sqrt2}{4} \frac{m}{s}\] \[x = 0.1 \qquad υ = 0 \qquad δεσμός\]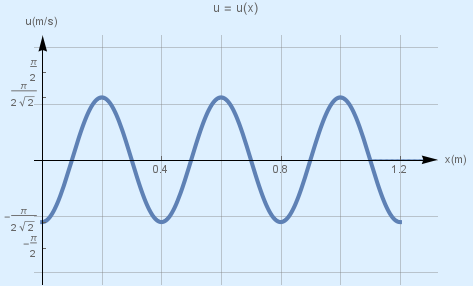

σχήμα

Θέμα Δ

Δ1

Για την ελεύθερη πτώση του σώματος $Σ_1$ εφαρμόζουμε την αρχή διατήρησης της μηχανικής ενέργειας έως τη χρονική στιγμή που το ελατήριο καρφώνεται στο $Σ_2$.

\[Κ_{αρχ} + U_{αρχ} = Κ_{τελ} + U_{τελ} \Rightarrow 0 + m_1 \cdot g \cdot h = \frac{1}{2} \cdot m \cdot υ_1^2 \Rightarrow υ_1 = \sqrt{2gh} = 2 \sqrt3 \frac{m}{s}\]

Για την απλή αρμονική ταλάντωση που εκτελεί το σώμα $Σ_1$ ισχύει:

\[D = k = m_1 \cdot ω^2 \Rightarrow ω = 5 \frac{rad}{s}, \qquad T = \frac{2π}{ω} = \frac{2π}{5} s\]

Δ2

Στην θέση ισορροπίας για την ταλάντωση του σώματος $Σ_1$ ισχύει:

\[ΣF = 0 \Rightarrow k\cdot x_1 = m \cdot g \Rightarrow x_1 = 0.4m\]

Εφαρμόζουμε την αρχή διατήρησης της ενέργειας ταλάντωσης για το σώμα $Σ_1$

\[Ε = Κ + U \Rightarrow \frac{1}{2} D \cdot A^2 = \frac{1}{2} m_1 \cdot υ_1^2 + \frac{1}{2} D \cdot x_1^2 \Rightarrow A = 0.8m\]

Την χρονική στιγμή $t=0$ το σώμα $Σ_1$ βρίσκεται στην θέση $x = +x_1$ και έχει αρνητική ταχύτητα.

\[y = A \cdot ημ(ωt + φ_ο) \Rightarrow +x_1 = A \cdot ημφ_ο \Rightarrow ημφ_ο = \frac{1}{2} \Rightarrow ημφ_ο = ημ\frac{π}{6}\]

η λύση της τριγωνομετρικής εξίσωσης μας δίνει:

\[φ_ο = 2kπ + \frac{π}{6} \overset{k=0}{\implies} \\\ φ_ο = \frac{π}{6} rad\]

που απορρίπτεται διότι η ταχύτητα είναι αρνητική οπότε

\[φ_ο = 2kπ + \frac{5π}{6} \overset{k=0}{\implies} \\\ φ_ο = \frac{5π}{6} rad\]

και η εξίσωση της απομάκρυνσης είναι:

\[y = 0.8 ημ(5t +\frac{5π}{6}) \qquad S.I.\]

Δ3

\[υ_{ηχ} = 340 \frac{m}{s} \qquad υ_{max} = ω \cdot A = 4 \frac{m}{s}\] \[f_{max} = \frac{υ_{ηχ}}{υ_{ηχ} - υ_{max}} \cdot f_s = 688,095 Hz\] \[f_{min} = \frac{υ_{ηχ}}{υ_{ηχ} + υ_{max}} \cdot f_s = 672,093 Hz\]

Δ4

Όταν το σώμα $Σ_1$ φτάνει στην πάνω ακραία θέση ταλάντωσης η δύναμη του ελατηρίου είναι:

\[F_{ελ} = k(A - x_1) = 40N\]

και η δύναμη που ασκεί το ελατήριο στο σώμα $Σ_2$ έχει το ίδιο μέτρο αλλά αντίθετη φορά, έτσι για το σώμα $Σ_2$ έχουμε:

\[F'_{ελ} = 40Ν > W_2 = m_2 \cdot g = 20N\]

και έτσι βγάζουμε το συμπέρασμα ότι το σώμα $Σ_2$ χάνει την επαφή του με το δάπεδο. Για το σώμα $Σ_1$ μόλις αποχωρίζεται το σώμα $Σ2$ από το δάπεδο ισχύουν:

\[ΣF = 0 \Rightarrow F'_{ελ} - W_2 = 0 \Rightarrow F'_{ελ} = 20Ν \Rightarrow k \cdot x_2 = 20N \Rightarrow x_2 = 0.2m\]

η δύναμη επαναφοράς για το σώμα $Σ_1$ είναι

\[F_{επ} = - D \cdot x = -100(0.4+0.2) = -60N\]

εφαρμόζουμε αρχή διατήρησης της ενέργειας ταλάντωσης για να υπολογίσουμε την ταχύτητα του σώματος $Σ_1$ την στιγμή που χάνεται η επαφή του σώματος $Σ_2$ από το δάπεδο.

\[\frac{1}{2} D \cdot A^2 = \frac{1}{2} m_1 υ^2 + \frac{1}{2} D (x_1+x_2)^2 \Rightarrow υ = \sqrt7 \frac{m}{s}\]

Άρα ο ζητούμενος ρυθμός μεταβολής της κινητικής ενέργειας είναι

\[\frac{ΔK}{Δt} = F \cdot υ \Rightarrow \frac{ΔK}{Δt} = -60 \cdot \sqrt7 \frac{J}{s}\]

Ο κώδικας σε mathematica για την εικόνα στο θέμα $Β_1$

f[x] := 0
g[x] := 2 * Pi
h[x] := 4 *Pi
k[x] := 15
j[x] := 0
	Show[{Plot[f[x], {x, 0, 3}, PlotStyle -> {Thickness[0.01]}],
		  Plot[g[x], {x, 3, 5}, PlotStyle -> {Thickness[0.008]}],
          Plot[k[x], {x, 0, 7},  PlotStyle -> Opacity[0.1]],
          Plot[j[x], {x, -0.3, 7}, PlotStyle -> Opacity[0.1]],
   		      Plot[h[x], {x, 5, 7}, PlotStyle -> {Thickness[0.008]}]},
	    		AxesStyle -> Arrowheads[0.04],
	    		Ticks -> { {3, 5}, {2Pi, 4Pi} },
        		PlotRange -> All,
 					GridLines -> Automatic,
 				Background -> LightBlue, 
 					PlotLabel -> "Umax = f(t)", 
 					AxesLabel -> {"t(s)","Umax(m/s)"}, 
 					AxesOrigin -> {0, 0},
 					Filling -> Automatic,
 					Epilog -> {Black, Text [O___], Point[{0, 0}]}]

Ο κώδικας σε mathematica για την εικόνα στο θέμα $Γ_3$

f[x] := 5.5*Pi - 5*Pi*x
g[x] := 0
k[x] := 19
j[x] := 0
Show[{Plot[f[x], {x, 0, 1.1}, PlotStyle -> {Thickness[0.01]}], 
      Plot[g[x], {x, 1.1, 1.5}, PlotStyle -> {Thickness[0]}]},
      Plot[k[x], {x, 0, 1.5},  PlotStyle -> Opacity[0.1]],
      Plot[j[x], {x, -0.2, 1.2}, PlotStyle -> Opacity[0.1]],
    		AxesStyle -> Arrowheads[0.04],
    		Ticks -> { {1.1, 1.2}, { 11Pi/2} },
    		PlotRange -> All,
 				GridLines -> Automatic,
 				Background -> LightBlue, 
 				PlotLabel -> "φ = φ(x)", 
 				AxesLabel -> {"x(m)","\[CurlyPhi](rad)"}, 
 				AxesOrigin -> {0, 0},
 				Filling -> Automatic]

Ο κώδικας σε mathematica για την εικόνα στο θέμα $Γ_4$

f[x] := 0.05*Sin[5.5Pi-5Pi*x]
g[x] := 0
k[x] := 0.07
j[x] := -0.07
Show[{Plot[f[x], {x, 0, 1.1}, PlotStyle -> {Thickness[0.01]}], 
      Plot[g[x], {x, 1.1, 1.2}, PlotStyle -> {Thickness[0.01]}]},
      Plot[k[x], {x, 0, 1.3},  PlotStyle -> Opacity[0]],
      Plot[j[x], {x, -0.1, 1.2}, PlotStyle -> Opacity[0]],
    		AxesStyle -> Arrowheads[0.04],
    		Ticks -> { {0.1, 0.7,0.3, 1.1, 1.2}, { -0.05, 0, 0.05} },
    		PlotRange -> All,
 				GridLines -> Automatic,
 				Background -> LightBlue, 
 				PlotLabel -> "στιγμιότυπο κύματος", 
 				AxesLabel -> {"x(m)","y(m)"}, 
 				AxesOrigin -> {0, 0},
 				Filling -> Automatic]

Ο κώδικας σε mathematica για την εικόνα στο θέμα $Γ_5$

f[x] := -(Pi/4) * Sqrt[2] *Cos[5Pi*x]
g[x] := 0
k[x] := 2
j[x] := -2
Show[{Plot[f[x], {x, 0, 1.2}, PlotStyle -> {Thickness[0.01]}], 
      Plot[g[x], {x, 1.1, 1.2}, PlotStyle -> {Thickness[0]}]},
      Plot[k[x], {x, 0, 1.2},  PlotStyle -> Opacity[0]],
      Plot[j[x], {x, 0, 1.2}, PlotStyle -> Opacity[0]],
    		AxesStyle -> Arrowheads[0.04],
    		Ticks -> { {0.4, 0.8, 1.2}, {Pi/2, (Sqrt[2] * Pi)/4, -(Sqrt[2] * Pi)/4, -Pi/2} },
    		PlotRange -> All,
 				GridLines -> Automatic,
 				Background -> LightBlue, 
 				PlotLabel -> "u = u(x)", 
 				AxesLabel -> {"x(m)","u(m/s)"}, 
 				AxesOrigin -> {0, 0},
 				Filling -> Automatic]

Λύση του συστήματος των εξισώσεων για το πρόβλημα των κεκλιμένων επιπέδων:

		Solve[{T1 == m*a, N1==m*g, 
				N2*Sin\[Theta] - T1== m*a, 
				N2*Cos\[Theta] == N1 + m*g, 
				N3 == N2*Cos\[Theta] + m*g, 
				F-N2*Sin\[Theta] == m*a}, 
				{T1, N1, N2, N3, F, a}] 

← Previous Archive Next →

blog comments powered by Disqus

Published

04 February 2018

Προσομοίωση 2018 ΓΕΛ Τριανδρίας, Χαλάστρας

Published

Category

Tags