Μοριοδότηση 2017
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(δ\)
Α2 - \(γ\)
Α3 - \(α\)
Α4 - \(δ\)
Α5: \(Λ - Σ - Σ - Σ - Λ\)
Θέμα Β
B1-\((ii)\)
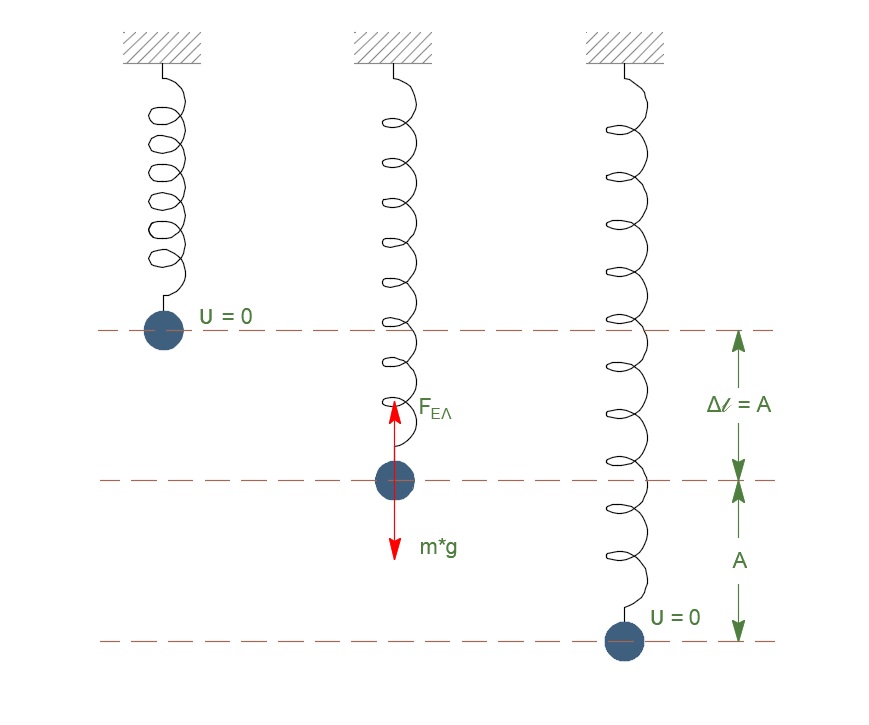
α) \(\underline {τρόπος}\)
\[m, αατ:\] \[(ΘΙ) ΣF=0 \Rightarrow \\ F_{ελ}-mg=0 \Rightarrow \\ kΔl=mg \Rightarrow \\ Δl=\frac{mg}{k}\]Επειδή στη ΘΦΜ \(v=0\), άρα \(Δl=A\)
\[U_{ελ_{max}}= U_{ελ(Γ')}=\frac{1}{2}k\left(2A\right)^2=\frac{1}{2}k4A^2=2k\frac{m^2g^2}{k^2}=\frac{2m^2g^2}{k}\]άρα σωστό το (ii)
β) \(\underline {τρόπος}\)
Θ.Μ.Κ.Ε από την θέση Φυσικού Μήκους στην ακραία απομάκρυνση
\[ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_F + W_B \Rightarrow 0 - 0 = - \frac{1}{2} \cdot k \cdot y^2 + m \cdot g \cdot y\] \[y(m \cdot g - \frac{1}{2} \cdot k \cdot y) = 0 \Rightarrow y = \frac{2 \cdot m \cdot g}{k}\] \[U_{ελ_{max}}= \frac{1}{2} \cdot k \cdot y^2 \Rightarrow U_{ελ_{max}} = \frac{2m^2g^2}{k}\]Β2 - \((ιιι)\)
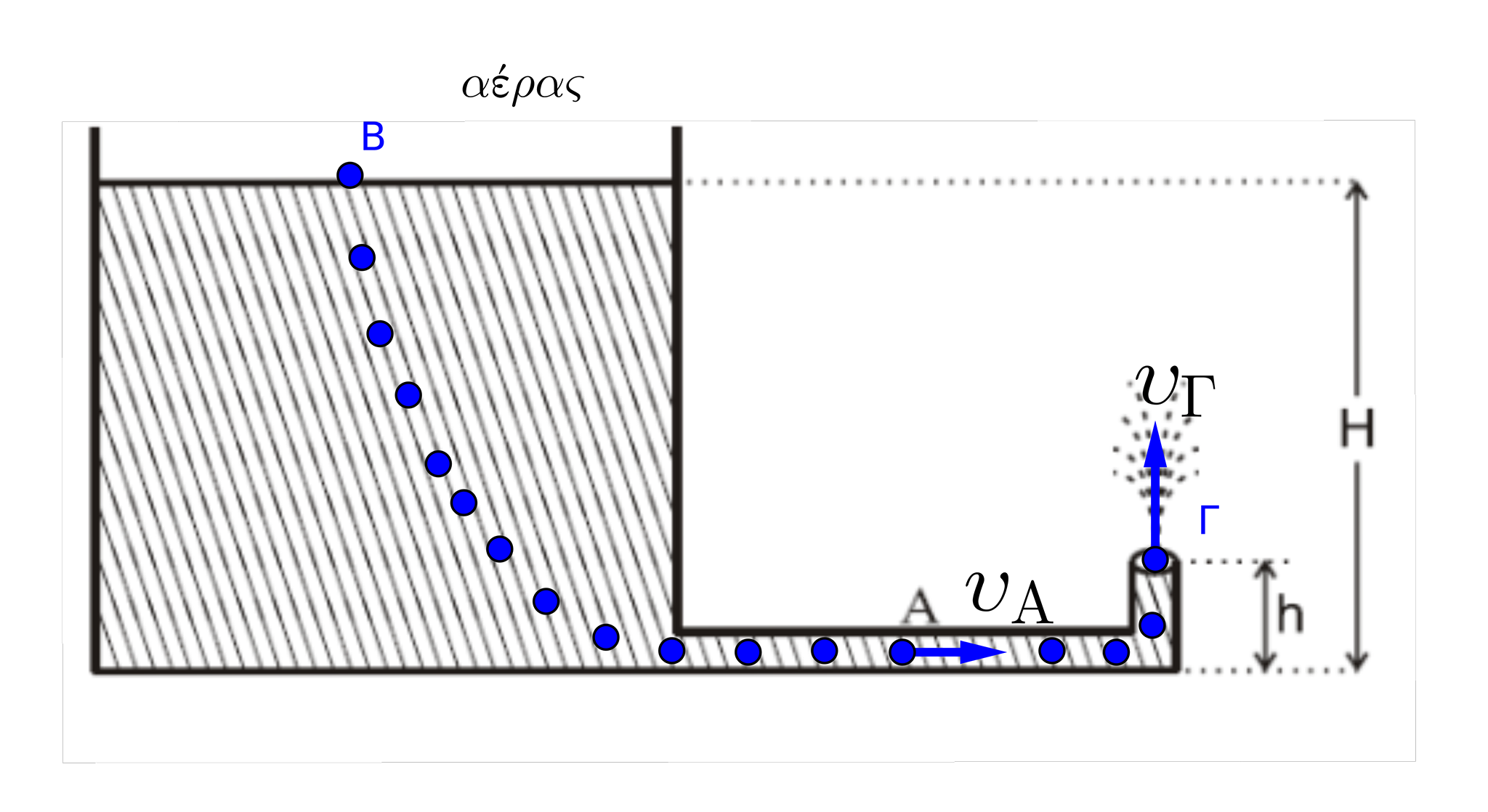
α) \(\underline {τρόπος}\)
Από εξίσωση Bernoulli: \(Β\to Γ\)
\[P_B + \frac{1}{2}ρv_Β^2+ρgH=P_Γ+\frac{1}{2}ρv_Γ^2+ρgh\overset{P_Β=P_Γ=P_{at}}{\underset{v_Β=0}{\implies}} \\\ ρg5h=\frac{1}{2}ρv_Γ^2+ρgh\Rightarrow v_Γ^2=8gh\Rightarrow v_Γ=2\sqrt{2gh}\]Σύμφωνα με την εξίσωση συνέχειας, η παροχή είναι ίδια για όλα τα σημεία του σωλήνα. Άρα η παροχή στα σημεία Α και Γ είναι
\[Π_Α = Π_Γ \Rightarrow A_A v_Α = Α_Γ v_Γ \Rightarrow v_Α = v_Γ = 2 \sqrt{2gh}\]άρα σωστό το (iii)
β) \(\underline {τρόπος}\)
Από εξίσωση Bernoulli: \(Α\to Γ\)
\[P_Α + \frac{1}{2}ρv_Α^2+0=P_Γ+\frac{1}{2}ρv_Γ^2+ρgh\overset{P_Γ=P_{at}}{\underset{v_A=v_Γ}{\implies}}\\\ P_A = P_{at} + ρgh\]Από εξίσωση Bernoulli: \(Β\to A\)
\[P_B + \frac{1}{2}ρv_Β^2+ρgH=P_A+\frac{1}{2}ρv_A^2+0 \Rightarrow P_B + \frac{1}{2}ρv_Β^2+ρg5h= P_{at} + ρgh + \frac{1}{2}ρv_Α^2\] \[ρg5h=\frac{1}{2}ρv_A^2+ρgh\Rightarrow v_A^2=8gh\Rightarrow v_A=2\sqrt{2gh}\]Β3 - \((ιι)\)
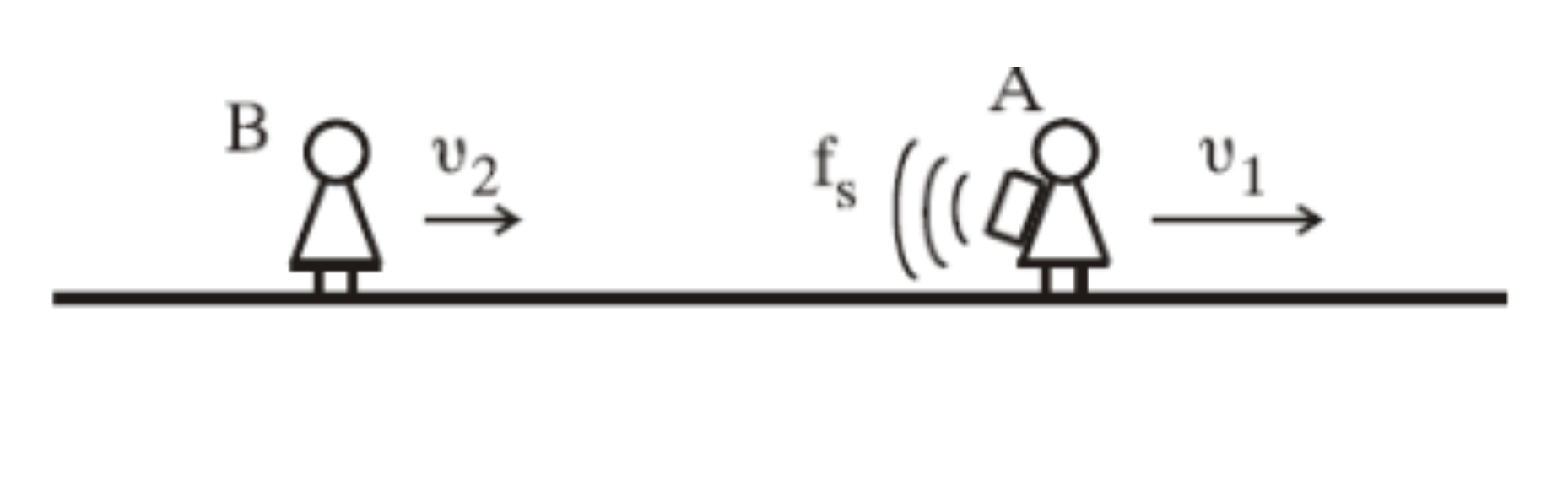
α) \(\underline {τρόπος}\)
Ο παρατηρητής \(Β\) πλησιάζει την πηγή \(Α\) και η πηγή απομακρύνεται από τον παρατηρητή \(Β\) άρα θα ισχύει
\[f_Β=\dfrac{v_{ηχ}+v_2}{v_{ηχ}+v_1}f_s=\dfrac{v_{ηχ}+\dfrac{v_{ηχ}}{10}}{v_{ηχ}+\dfrac{v_{ηχ}}{5}}f_s=\dfrac{\dfrac{11v_{ηχ}}{10}}{\dfrac{6v_{ηχ}}{5}}f_s=\dfrac{11\cdot5}{10\cdot6}f_s=\dfrac{11}{12}f_s\]άρα σωστό το (ii)
β) \(\underline {τρόπος}\)
Όταν ο παρατηρητής \(Β\) πλησιάζει προς την πηγή φτάνουν σε αυτόν περισσότερα μέγιστα στη μονάδα του χρόνου απο όσα παράγει στον ίδιο χρόνο η πηγή. Η ταχύτητα με την οποία διαδίδεται ο ήχος ως προς τον παρατηρητή είναι \(v_{ηχ} + v_2\) και η συχνότητα που αντιλαμβάνεται ο παρατηρητής είναι
\[f_B = \frac{v_{ηχ}+v_2}{v}\cdot f_s\]Όταν η πηγή απομακρύνεται από τον παρατηρητή, η ταχύτητα με την οποία διαδίδεται ο ήχος ως προς τον αέρα θα είναι πάλι \(v_{ηχ}\), αφού εξαρτάται μόνο από το μέσον διάδοσης, ενώ το μήκος κύματος που φτάνει στον παρατηρητή αυξάνεται. Ο χρόνος που μεσολαβεί ανάμεσα στην εκπομπή δύο μεγίστων είναι μία περίοδος \(Τ\). Αν τη στιγμή \(t\) η πηγή εκπέμπει ένα μέγιστο, τη στιγμή \(t+Δt\) το μέγιστο θα έχει απομακρυνθεί από τον παρατηρητή κατά \(λ\) αλλά και η πηγή θα έχει απομακρυνθεί κατά \(v_1\cdot Τ\). Η απόσταση ανάμεσα στα δυο διαδοχικά μέγιστα είναι \(λ+v_1 \cdot T\). Αυτή την απόσταση αντιλαμβάνεται ως μήκος κύματος ο παρατηρητής. Επομένως
\[λ_Β = λ + v_1 \cdot T \Rightarrow λ_Β = \frac{v_{ηχ}}{f_s}+\frac{v_1}{f_s}\] \[f_B = \frac{v_{ηχ}}{λ_Β} \Rightarrow f_B = \frac{v_{ηχ}}{\frac{v_{ηχ}+v_1}{f_s}} \Rightarrow f_B = \frac{v_{ηχ}}{v_{ηχ}+v_1} \cdot {f_s}=\]Συνθέτοντας τις δύο περιπτώσεις κίνησης αφού και η πηγή και ο παρατηρητής κινούνται σε σχέση με το μέσον διάδοσης, η συχνότητα που αντιλαμβάνεται ο παρατηρητής είναι
\[f_Β=\dfrac{v_{ηχ}+v_2}{v_{ηχ}+v_1}f_s\]Θέμα Γ
Γ1
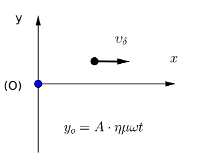
σε \(Δt\) η διαταραχή διαδόθηκε σε απόσταση \(Δx=4cm=0,04m\).
\[v_δ=\frac{Δx}{Δt}=\frac{0,04}{0,4}=0,1m/s\] \[v_δ=\frac{λ}{T}\Rightarrow λ=0,08m\]Το \(Δm\) εκτελεί α.α.τ.:
\[D=Δm\cdot ω^2=Δm\frac{4\pi^2}{T^2}=10^{-6}\frac{4\pi^2}{0,64}= \frac{\pi^2}{16}10^{-4}\frac{N}{m}\] \[E_T=\frac{1}{2}D\cdot A^2\Rightarrow 5\pi^2 10^{-7}=\frac{1}{2}\cdot\frac{\pi^2}{16}10^{-4}A^2\] \[A^2=0,16\Rightarrow A=0,4m \text{ (πλάτος)}\]Γ2
Η εξίσωση του κύματος είναι:
\[y_{(x,t)}=Aημ\left(\frac{2\pi t}{T}-\frac{2\pi x}{λ}\right)=0,4ημ\left(\frac{5\pi t}{2}-25\pi x \right) \text{ (SI)}\]Στιγμιότυπο την \(t_1=1,4s\):
Την \(t_1\) η διαταραχή έφτασε στη θέση
α) \(\underline {τρόπος}\)
\[x_1=v_δ t_1=0,1\cdot 1,4=0,14m, N_1=\frac{x_1}{λ}=\frac{0,14}{0,08}=\frac{14}{8}=\frac{7}{4} \text{ μήκη κύματος}\]β) \(\underline {τρόπος}\)
\[φ_{t_1}=0\Rightarrow \frac{5\pi \cdot 1,4}{2}-25\pi x_1=0\Rightarrow x_1=0,14m\]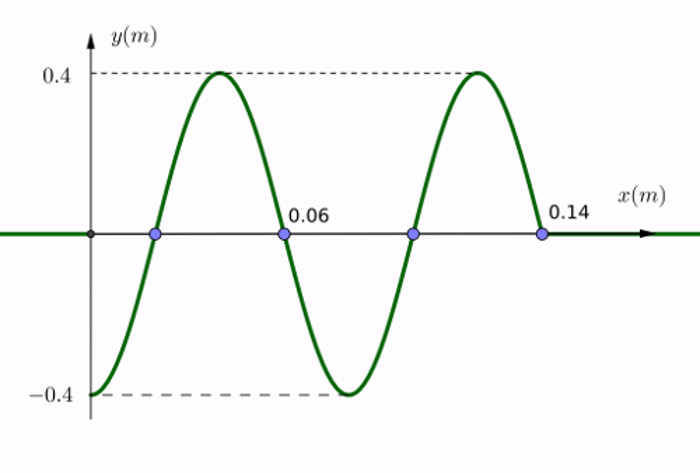
Γ3
α) \(\underline {τρόπος}\)
\(ΑΔΕ_{ταλ}\) για \(Δm\)
Για \(y=0,2m=\frac{A}{2}\)
\[E_T=K+U\Rightarrow E_T=K+\frac{1}{2}Dy^2 \overset{y=\frac{A}{2}}{\implies} E_T=K+\frac{1}{2}D\frac{A^2}{4}\Rightarrow \\\ E_T=K+\frac{1}{4}E_T\Rightarrow K=\frac{3}{4}E_T=\frac{3}{4}5\pi^2 10^{-7}=\frac{3\pi^2}{8}10^{-6} J\]β) \(\underline {τρόπος}\)
\[y=Aημφ=\frac{A}{2}\Rightarrow ημφ=\frac{1}{2}\Rightarrow φ=\begin{cases}2k\pi+\frac{\pi}{6}, & k=0,1,2,... (1) \\\ 2k\pi + \frac{5\pi}{6}, & k = 0,1,2,... (2)\end{cases}\] \[v=ωAσυνφ=\begin{cases}=ωAσυν\left(2k\pi+\frac{\pi}{6}\right)=\frac{ωA\sqrt{3}}{2} \\\ ωAσυν\left(2k\pi+\frac{5\pi}{6}\right)=-\frac{ωA\sqrt{3}}{2}\end{cases}\] \[K=\frac{1}{2}Δm\cdot v^2=\frac{1}{2}Δm\left(\pm \frac{ωA\sqrt{3}}{2} \right)^2=\frac{1}{2}Δm\cdot \frac{ω^2A^2 3}{4}=\frac{3}{4}\cdot\frac{1}{2}D\cdot A^2=\frac{3}{4}E_T\]Γ4
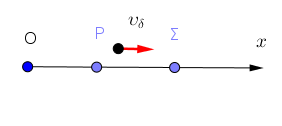
α) \(\underline {τρόπος}\)
\[φ_Ρ-φ_Σ=\frac{3\pi}{2}rad,(φ_Ρ>φ_Σ)\] \[\left. \begin{matrix}y_Ρ=0,4m=A \\\\ y_Ρ=Aημφ_Ρ\end{matrix} \right\} ημφ_Ρ=1\implies φ_Ρ=2k\pi+\frac{\pi}{2},k=0,1,2,\ldots\] \[2k\pi+\frac{\pi}{2}-φ_Σ=\frac{3\pi}{2}\Rightarrow φ_Σ=2k\pi-\pi\]Άρα
\[v_Σ=\frac{5\pi}{2}\cdot 0,4\cdot συν\left(2k\pi-\pi\right)\Rightarrow v_Σ=-\pi \frac{m}{s}\]β) \(\underline {τρόπος}\)
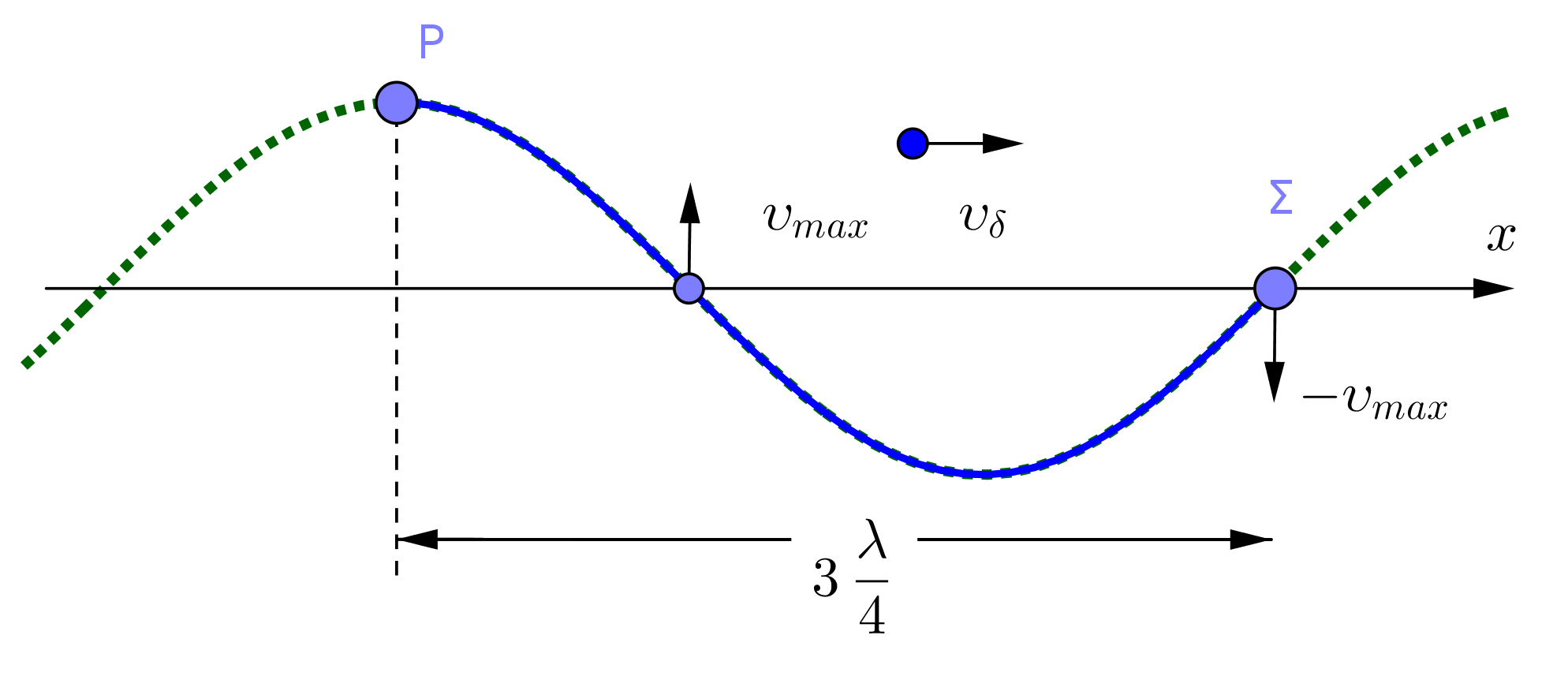
όταν \(y_Ρ=A\), \(v_Σ=-ωA=-\pi \frac{m}{s}\)
γ) \(\underline {τρόπος}\)
\[φ_Ρ-φ_Σ=\frac{3\pi}{2}\Rightarrow φ_Σ = φ_Ρ - \frac{3\pi}{2}\] \[y_Ρ = Α \cdot ημφ_Ρ \Rightarrow ημφ_Ρ = 1\] \[v_Σ = Αωσυνφ_Σ = Αωσυν(φ_Ρ - \frac{3\pi}{2}) = -Αωημφ_Ρ \Rightarrow v_Σ = - \pi \frac{m}{s}\]δ) \(\underline {τρόπος}\)
Κάθε μέγεθος που μεταβάλλεται αρμονικά με τον χρόνο μπορεί να αναπαρασταθεί με ένα περιστρεφόμενο διάνυσμα, το οποίο περιστρέφεται σε σταθερή γωνιακή ταχύητα \(ω\) και η προβολή του στον κατακόρυφο άξονα \(yy'\) δίνεται από την σχέση \(y = Aημωt\).
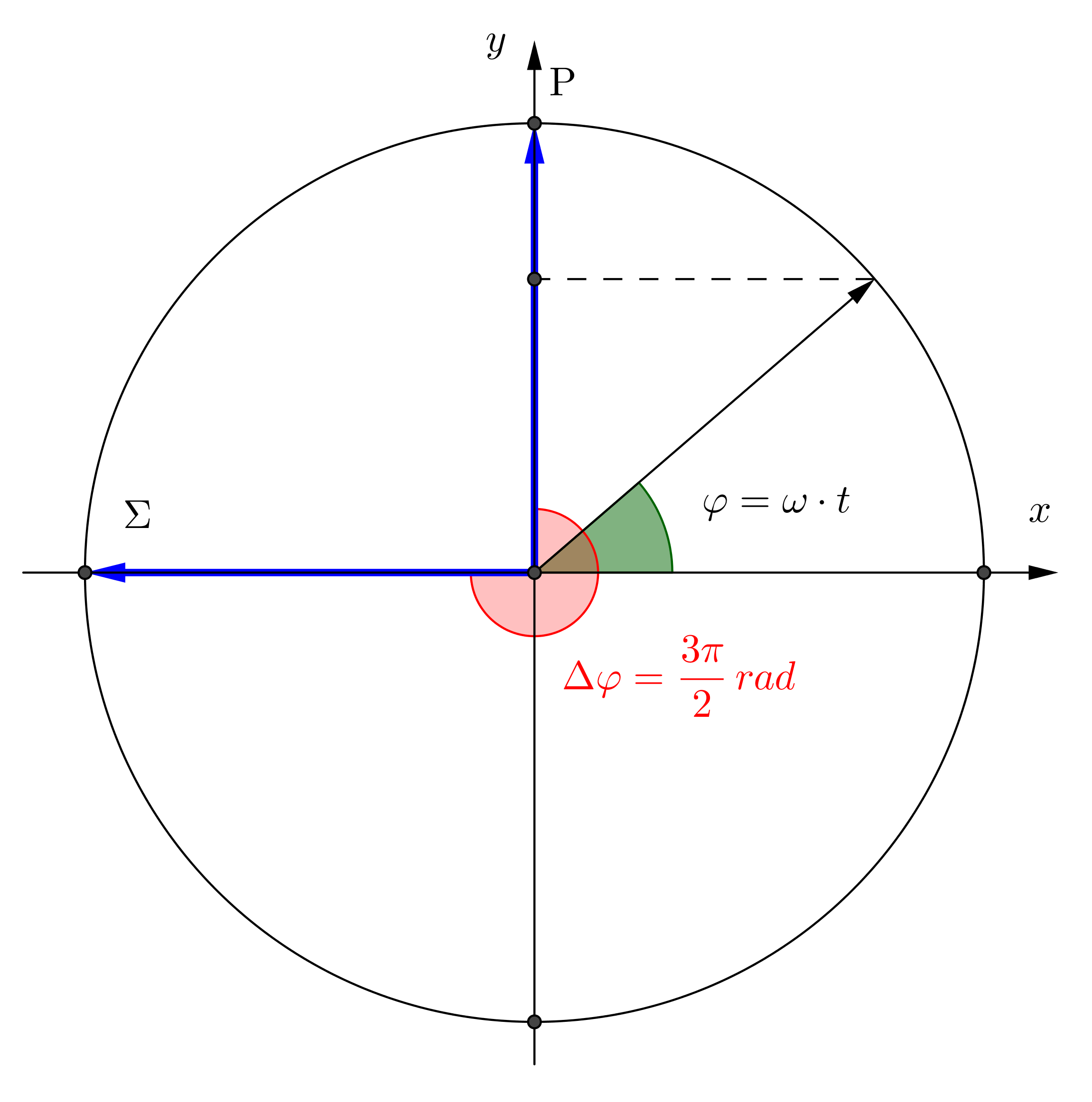
Η διαφορά φάσης των δύο περιστρεφόμενων διανυσμάτων είναι
\[Δφ = \frac{3\pi}{2} rad\]από το σχήμα βγαίνει το συμπέρασμα ότι το σημείο \(Σ\) βρίσκεται στην θέση ισορροπίας του και κινείται με φορά προς τον αρνητικό ημιάξονα.
Άρα \(v_Σ = -\pi \frac{m}{s}\)
Θέμα Δ
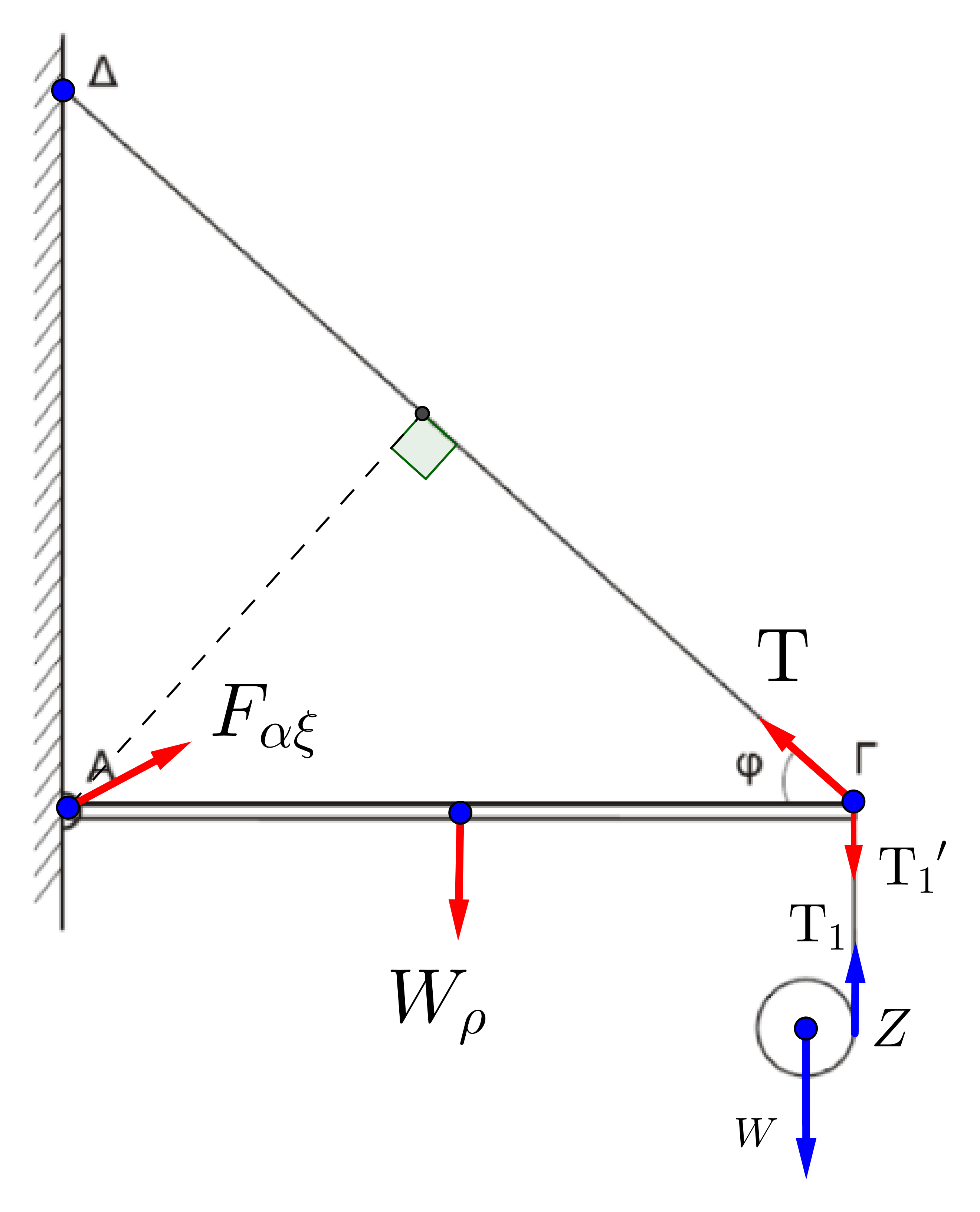
Δ1
α) \(\underline {τρόπος}\)
\[0=v_Γ=v_Z=v_{cm}-v_{γρ_Ζ}\Rightarrow v_{cm}=ωR\Rightarrow a_{cm}= a_{γων} \cdot R\]Ροπή αδράνειας του δίσκου ως προς το σημείο \(Ζ\) με θεώρημα Steiner
\[I_Z = I_{cm} + m \cdot R^2 \Rightarrow I_Z = \frac{1}{2} \cdot m \cdot R^2 + m \cdot R \Rightarrow I_Z = \frac{3}{2}\cdot m \cdot R^2\] \[Στ_Ζ = Ι_Ζ \cdot α_{γων} \Rightarrow m \cdot g \cdot R = \frac{3}{2}\cdot m \cdot R^2 \cdot α_{γων} \Rightarrow α_{cm} = \frac{2g}{3} \Rightarrow α_{cm} = \frac{20}{3} \frac{m}{s^2}\]β) \(\underline {τρόπος}\)
\[\left. \begin{matrix}ΣF=m\cdot a_{cm}\Rightarrow W-T_1=m\cdot a_{cm} \\\ Σ τ=Iα_{γων}\Rightarrow T_1\cdot R=\frac{1}{2}mR^2\cdot α_{γων}\end{matrix} \right\} \\\ T_1=\frac{m\cdot a_{cm}}{2},W=\frac{3m\cdot a_{cm}}{2}\] \[0=v_Γ=v_Z=v_{cm}-v_{γρ_Ζ}\Rightarrow v_{cm}=ωR\Rightarrow a_{cm}= \\\ a_γ R\Rightarrow a_{cm}=\frac{2}{3}g=\frac{20}{3}\frac{m}{s^2}\]Δ2
\[ΣF = 0 \Rightarrow T'_1=T_1=\frac{2\cdot 20}{2\cdot 3}=\frac{20}{3}N\]3ος Νόμος του Νεύτωνα και νήμα αβαρές μη εκτατό.
Για τη ράβδο που ισορροπεί:
\[Σ_{τ_{(Α)}}=0\Rightarrow w_ρ\cdot\frac{l}{2}+T'_1\cdot l-T\cdot l\cdot ημφ=0\Rightarrow T=\frac{100}{3}N\]Δ3
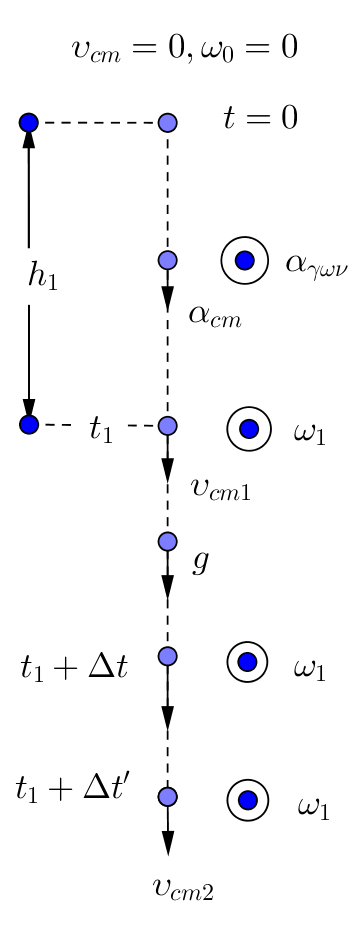
α) \(\underline {τρόπος}\)
Την \(t_1\), \(h_1=0,3m\)
\[h_1=\frac{1}{2}a_{cm}t_1^2\Rightarrow 0,3=\frac{1}{2}\cdot\frac{20}{3}t_1^2\Rightarrow t_1=0,3s\] \[a_{γων}=\frac{a_{cm}}{R}=\frac{200}{3}r/s^2\] \[w_1=a_{γων}t_1=20r/s\] \[t \to t_1+Δt:\] \[τ_{w_{cm}}=0=\frac{ΔL}{Δt}\Rightarrow L_{t_1}=L_{t_1+Δ_t}\]Η μόνη δύναμη που ασκείται στο δίσκο είναι το βάρος \(W\). Όπου
\[L_{t_1}=I\cdot ω_1\] \[I=\frac{1}{2}mR^2=\frac{1}{2}\cdot 2 \cdot 0,1^2=0,01kg m^2\]Άρα
\[L_{t_1}=0,2kg\frac{m^2}{s}=L_{t_1+Δt}\]β) \(\underline {τρόπος}\)
\[ΘΜΚΕ_{(0\to h_1)}:\] \[\left. \begin{matrix}\text{μετ: }\frac{1}{2}mv_{cm1}^2-0=W\cdot h_1-T_1\cdot h_1 \\\ \text{στρ: } \frac{1}{2}Iω_1^2-0=+(T_1\cdot R)\cdot θ_1 \\\ v_{cm1}=ω_1\cdot R \\\ x_{cm}=θ\cdot R\Rightarrow h_1=θ_1\cdot R \end{matrix} \right\}\Rightarrow \\\ \frac{1}{2}mv_{cm1}^2+\frac{1}{2}Iω_1^2=mgh_1\Rightarrow \\\ \frac{1}{2}v_{cm1}^2+\frac{1}{4}\cdot v_{cm1}^2=gh_1 \Rightarrow v_{cm1}^2=\frac{4gh_1}{3}\Rightarrow \\\ v_{cm1}=2m/s \Rightarrow ω_1=20r/s \\\ \Rightarrow L_{t_1}=Iω_1=0,2kg \frac{m^2}{s}\Rightarrow L_{t_1}=0,2 kg \frac{m^2}{s}\]γ) \(\underline {τρόπος}\)
Η δύναμη \(T_1\) δε μετατοπίζει το σημείο εφαρμογής της, αφού κάθε στιγμή ασκείται σε διαφορετικό σημείο του δίσκου, λειτουργεί δηλαδή όπως η στατική τριβή στη Κ.Χ.Ο. Επομένως η μηχανική ενέργεια του δίσκου διατηρείται.
\[ΑΔΜΕ_{(0,h_1)}:\] \[K_{(0)}+U_{(0)}=K_{(t_1)}+U_{(t_1)} \Rightarrow 0+mgh_1=( \frac{1}{2}mv_{cm1}^2+\frac{1}{2}Iω_1^2) + 0\] \[mgh_1=\frac{1}{2}mω_1^2R^2+\frac{1}{2}Iω_1^2 \Rightarrow mgh_1=Iω_1^2+\frac{1}{2}Iω_1^2=3\cdot\frac{1}{2}Iω_1^2\] \[K_{στρ}=\frac{1}{2}Iω_1^2\] \[L=Iω_1 \Rightarrow K_{στρ}=\frac{L^2}{2I}\] \[mgh_1=3K_{(στρ)} \Rightarrow mgh_1=\frac{3L^2}{2I} \Rightarrow 9\cdot 10\cdot 0,3=\frac{3L_{t_1}^2}{2\cdot 0,01} \Rightarrow L_{t_1}=0,2kg \frac{m^2}{s}\]Δ4
\[t_2=t_1+Δt:\] \[\frac{K_{στρ(t_2)}}{K_{μετ(t_2)}}=\frac{\frac{1}{2}Iω_2^2}{\frac{1}{2}mv_{cm_2}^2}\] \[t_1=t_2:\] \[Στ_{cm}=0\Rightarrow ω_2=ω_1=20r/s \\\ ΣF=m\cdot a_{cm}\Rightarrow W=m\cdot a_{cm}\Rightarrow a_{cm}=g=10 m/s^2 \\\ v_{cm_2}=v_{cm_1}+g\cdot Δt'=2+10\cdot 0,1=3m/s\] \[\frac{K_{περ}}{K_{μετ}}=\frac{\frac{1}{2}Iω^2}{\frac{1}{2}mv^2}=\frac{\frac{1}{2}mR^2ω_2^2}{mv_2^2}=\frac{2}{9} \\\ \frac{K_{περ}}{K_{μετ}}=\frac{2}{9}\]Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus