Πανελλαδικές 2015
Από το εσωτερικό άκρο Α ενός ημισφαιρίου ακτίνας \(R=1,6m\) αφήνεται να κυλήσει μία συμπαγής μικρή σφαίρα μάζας \(m=1,4Kg\) και ακτίνας \( r = \frac{R}{8}\). Το ημισφαίριο είναι βυθισμένο στο έδαφος, όπως φαίνεται στο Σχήμα 3, και η κίνηση της σφαίρας γίνεται χωρίς ολίσθηση.
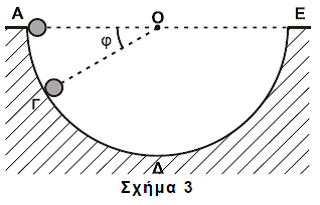
Δ1. Να εκφράσετε τη στατική τριβή \(T_s\) που ασκείται στη σφαίρα σε συνάρτηση με το συνημίτονο της γωνίας \(φ\) που σχηματίζει η ακτίνα ΟΓ του ημισφαιρίου με την ευθεία ΑΕ της επιφάνειας του εδάφους.
Δ2. Να υπολογίσετε την κάθετη δύναμη που ασκεί η ημισφαιρική επιφάνεια στη σφαίρα όταν αυτή βρίσκεται στο σημείο Γ όπου \(φ=30^o\) (Σχήμα 3).
Μια άλλη σφαίρα, όμοια με την προηγούμενη, εκτοξεύεται από το κατώτατο σημείο Δ του ημισφαιρίου με ταχύτητα \(υ=6m/s\) και κυλίεται χωρίς ολίσθηση στο εσωτερικό του με κατεύθυνση το άκρο Ε (Σχήμα 4).
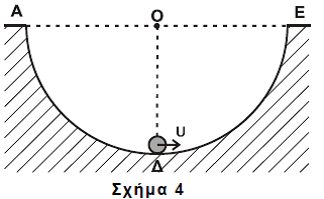
Δ3. Να υπολογίσετε το μέγιστο ύψος από την επιφάνεια του εδάφους που θα φτάσει η σφαίρα κατά την κίνησή της.
Δ4. Να υπολογίσετε τον ρυθμό μεταβολής της κινητικής ενέργειας (μονάδες 4) και το ρυθμό μεταβολής της στροφορμής της σφαίρας (μονάδες 2), αμέσως μόλις αυτή χάσει την επαφή με την επιφάνεια του ημισφαιρίου στο σημείο Ε.
Δίνονται: ροπή αδράνειας της σφαίρας ως προς άξονα που διέρχεται από το κέντρο μάζας \(I = \frac{2}{5} \cdot m \cdot r^2\) και η επιτάχυνση της βαρύτητας \(g=10m/s^2\)
Δ1. Το περιβάλλον για την σφαίρα όπως φαίνεται στο παρακάτω σχήμα
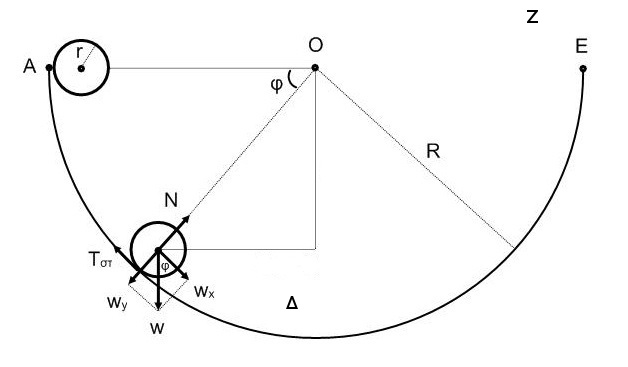
αποτελούν η γη και το βυθισμένο ημισφαίριο. Η γη ασκεί την δύναμη \(W\) που αναλύεται στις συνιστώσες \(W_x = m \cdot g \cdot συνφ\) και \(W_y = m \cdot g \cdot ημφ\). Το βυθισμένο ημισφαίριο ασκεί την κάθετη αντίδραση \(Ν\) και την στατική τριβή \(T_σ\). Ο δεύτερος νόμος του Νεύτωνα για τον άξονα x είναι:
\[ΣF_x = W_x - T_σ = m \cdot {α}_{cm}\]όπου \({α}_{cm}\) η επιτάχυνση του κέντρου μάζας. Ο δεύτερος νόμος του Νεύτωνα για την στροφική κίνηση είναι:
\[Στ = T_σ \cdot r = \frac{2}{5} \cdot m \cdot r^2 \cdot {α}_{γων}\]και επειδή έχουμε κύλιση χωρίς ολίσθηση ισχύει
\[{α}_{cm} = {α}_{γων} \cdot r\]οπότε
\[Τ_σ = \frac{2}{5} \cdot m \cdot {α}_{cm}\]Λύνοντας το σύστημα των δύο εξισώσεων έχουμε:
\[{α}_{cm} = \frac{5}{7} \cdot g \cdot συνφ\] \[T_σ = 4 \cdot συνφ\]Δ2. Επειδή έχουμε κυκλική κίνηση η συνισταμένη στον άξονα y παίζει τον ρόλο της κεντρομόλου δύναμης. Έτσι για \(φ=30^0\) έχουμε:
\[ΣF_y = N - W_y = \frac {m \cdot {v}_{cm}^2}{R-r}\]Για να υπολογίσουμε την ταχύτητα του κέντρου μάζας \({v}_{cm}\) θα χρησιμοποιήσουμε την αρχή διατήρησης της μηχανικής ενέργειας. Το βάρος είναι συντηρητική δύναμη, ενώ οι δυνάμεις που ασκεί το βυθισμένο ημισφαίριο στην σφαίρα δεν αυξάνουν, ούτε ελαττώνουν την ενέργεια της σφαίρας οπότε το έργο τους κατά μήκος κλειστής διαδρομής είναι για αυτή την περίπτωση μηδέν.
\[K_A + U_A = K_Γ + U_Γ\]Θεωρούμε επίπεδο μηδενικής δυναμικής ενέργειας το έδαφος, δηλαδή την ευθεία ΑΕ, οπότε κάνοντας αντικατάσταση στην αρχή διατήρησης της μηχανικής ενέργειας έχουμε:
\[0 + 0 = (\frac{1}{2} \cdot m \cdot {v}_{cm}^2 + \frac{1}{2} \cdot I \cdot ω^2) - m \cdot g \cdot (R-r) \cdot ημφ\]και μετά τις αντικαταστάσεις και τις πράξεις \({v}_{cm} = \sqrt{10} \frac{m}{s}\) Οπότε για την κάθετη δύναμη
\[N = m \cdot g \cdot ημφ + \frac {m \cdot {v}_{cm}^2}{R-r}\]μετά τις πράξεις N = 17N.
Δ3. Στο σημείο Δ έχουμε κύλιση χωρίς ολίσθηση δηλαδή
\[v_Δ = ω_Δ \cdot r\] \[ω_Δ = \frac{v_Δ}{r} \Rightarrow ω_Δ = 30 \frac {r}{s}\]Εφαρμόζουμε την αρχή διατήρησης της μηχανικής ενέργειας από την θέση Δ έως την θέση Ε για να υπολογίσουμε την ταχύτητα του κέντρου μάζας της σφαίρας στην θέση Ε, θεωρώντας ως επίπεδο μηδενικής δυναμικής ενέργειας το επίπεδο που διέρχεται από το κέντρο μάζας της σφαίρας στην κατακόρυφη θέση Δ.
\[K_Δ + U_Δ = K_Ε + U_Ε\] \[(\frac{1}{2} \cdot m \cdot v_Δ^2 + \frac{1}{2} \cdot I \cdot ω_Δ^2) +0 = (\frac{1}{2} \cdot m \cdot v_Ε^2 + \frac{1}{2} \cdot I \cdot ω_Ε^2) + m \cdot g \cdot (R-r)\]και μετά τις αντικαταστάσεις έχουμε \(v_E = 4 \frac{m}{s}\)
Από το σημείο Ε έως το σημείο Ζ, περιβάλλον για την σφαίρα αποτελεί μόνο η γη, οπότε η μόνη δύναμη που ασκείται στην σφαίρα είναι το βάρος. Αυτό σημαίνει ότι το αλγεβρικό άθροισμα των ροπών ως προς άξονα που διέρχεται από το κέντρο μάζας της σφαίρας είναι μηδέν, αφού το βάρος ασκείται στο κέντρο μάζας της σφαίρας. Δηλαδή η σφαίρα κινείται με σταθερή γωνιακή ταχύτητα.
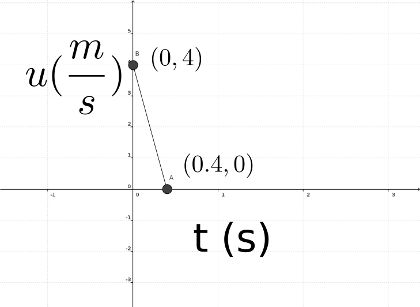
Στο παραπάνω σχήμα φαίνεται η γραφική παράσταση της ταχύτητας του κέντρου μάζας της σφαίρας σε συνάρτηση με το χρόνο.
\[v = v_0 - g \cdot t \Rightarrow v = 4 - 10 \cdot t\]Από το εμβαδόν του τριγώνου που σχηματίζεται υπολογίζεται το ζητούμενο ύψος από την επιφάνεια του εδάφους (\(h=0,8m\)).
Δ4. Αφού έχει χαθεί ήδη η επαφή με το βυθισμένο ημισφαίριο η μόνη δύναμη που ασκείται στην σφαίρα είναι η έλξη της γης άρα για τους ρυθμούς μεταβολής της κινητικής ενέργειας και της στροφορμής θα έχουμε:
\[\frac{dK}{dt} = ΣF \cdot v = - m \cdot g \cdot \cdot v_E\] \[\frac{dL}{dt} = Στ\]και μετά τις αντικαταστάσεις
\[\frac{dK}{dt} = -56 \frac{joule}{s}\] \[\frac{dL}{dt} = 0\]blog comments powered by Disqus