Ρυθμός μεταβολής στροφορμής
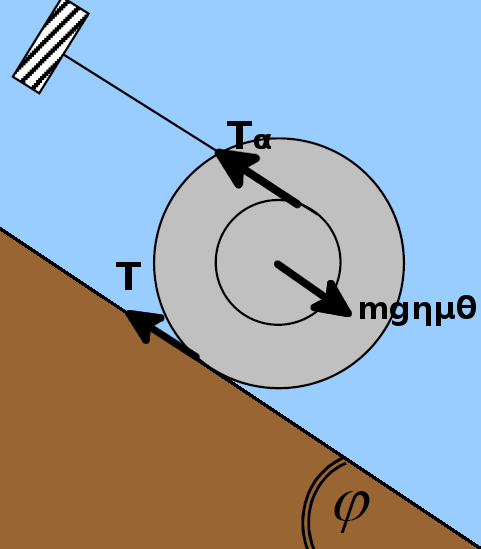
Στο σχήμα φαίνονται η συνιστώσα του βάρους
\[W_x = m \cdot g \cdot ημθ\]η τάση του νήματος \(Τ_α\) και η τριβή ολίσθησης
\[Τ = μ_s \cdot m \cdot g \cdot συνθ\]Η συνιστώσα του βάρους \(W_y\) και η κάθετη αντίδραση \(Ν\) είναι ίσες κατά μέτρο και με αντίθετες φορές, οπότε δεν σχεδιάστηκαν. Η ταχύτητα του κέντρου μάζας του κυλίνδρου είναι
\[υ_{cm} = 4 \frac{m}{s}\]και η γωνιακή ταχύτητα
\[ω = 80 \frac{rad}{s}\]Δηλαδή για την μεταφορική κίνηση η επιτάχυνση είναι
\[α = 0.4 \frac{m}{s^2}\]και για την περιστροφική κίνηση η γωνιακή επιτάχυνση είναι
\[α_{γων} = 8 \frac{rad}{s^2}\]H ακτίνα του μικρού κύκλου είναι \(r = \frac{R}{2}\) και η ακτίνα του μεγάλου κύκλου είναι \(R = 0.1m\) Δίνονται
\(ημθ = 0.6\), \(συνθ = 0.8\), \(g = 10 \frac{m}{s^2}\)
Να υπολογίσετε τον ρυθμό μεταβολής της στροφορμής του κυλίνδρου.
Απάντηση:
Ο ρυθμός μεταβολής της στροφορμής την συγκεκριμένη χρονική στιγμή ως προς το σημείο Κ είναι:
\[\frac{dL}{dt} = Στ = m \cdot g \cdot ημθ \cdot \frac{R}{2} - T \cdot \frac{3R}{2} = 0.3 - 0.24 = 0.06 kg \frac{m^2}{s^2}\]Θα κάνουμε τον ίδιο υπολογισμό θεωρώντας ότι η κίνηση του κυλίνδρου είναι σύνθετη αποτελούμενη από μια ιδιοπεριστροφή (spin) γύρω από άξονα που περνά από το κέντρο μάζας του κυλίνδρου και μια περιφορά γύρω από άξονα που περνά από το σημείο Κ (θεωρούμε σε αυτή την περίπτωση όλη την μάζα του κυλίνδρου συγκεντρωμένη στο κέντρο μάζας του).
Και στις δυο κινήσεις ο ρυθμός μεταβολής της στροφορμής είναι ένα διάνυσμα κάθετο στη σελίδα και με φορά προς τον αναγνώστη, δηλαδή και για τις δυο κινήσεις η περιστροφή γίνεται αντίθετα από τους δείκτες του ρολογιού.
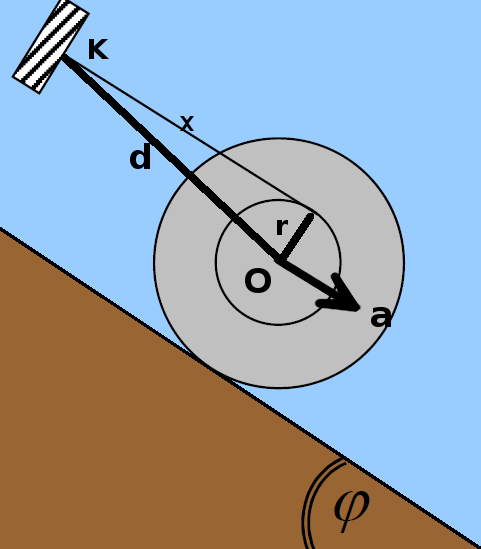
\[\frac{dL}{dt}_{spin} = I \cdot α_{γων} = \frac{1}{2} \cdot m \cdot R^2 \cdot α_{γων} = 0.04 kg \frac{m^2}{s^2}\] \[\frac{dL}{dt}_{περιφορά} = Ι_k \cdot α'_{γων}\]όπου \(I_k\) είναι η ροπή αδράνειας ως προς το σημείο Κ. Με την βοήθεια του δεύτερου σχήματος υπολογίζουμε το \(d\), αφού πρώτα βρούμε το x από την μεταφορική κίνηση του κυλίνδρου
\[x= \frac{1}{2} \cdot α \cdot t^2 = 20m\]Οπότε το \(d\) ως υποτείνουσα του ορθογωνίου τριγώνου είναι \(d = \sqrt{x^2 + r^2} = 20.0000624999m\)
\[I_k = I_{cm} + m \cdot d^2 = \frac{1}{2} \cdot m \cdot R^2 + m \cdot d^2 = 400.0075 kg \cdot m^2\]Και τώρα ο υπολογισμός του \(α'_{γων}\). Θεωρούμε ότι ο κύλινδρος είναι υλικό σημείο και η μάζα του είναι συγκεντρωμένη στο κέντρο μάζας του. Θα αναλύσουμε το διάνυσμα της επιτάχυνσης του κέντρου μάζας του \(α\) σε δυο συνιστώσες. Μία κατά την διεύθυνση που διέρχεται από το σημείο Κ και το κέντρο Ο και μία κάθετη στην παραπάνω διεύθυνση. Η πρώτη συνιστώσα δεν μας ενδιαφέρει. Είναι δηλαδή η περίπτωση όπου το υλικό σημείο απλά απομακρύνεται “ακτινικά” από το σημείο Κ, και άρα δεν περιστρέφεται. Για την δεύτερη συνιστώσα έχουμε:
\[α_x = α \cdot ημθ = 0,00099999687 \frac{m}{s^2}\]όπου η γωνία θ μπορεί να βρεθεί από το ορθογώνιο τρίγωνο του παραπάνω σχήματος \(ημθ = \frac{r} {d}\)
η γωνιακή επιτάχυνση \(α'_{γων}\) βρίσκεται από την σχέση
\[α_x = α'_{γων} \cdot d \Rightarrow α'_{γων} = \frac{α_x}{d} = 0.00004999828 \frac{rad}{s^2}\]και τελικά
\[\frac{dL}{dt}_{περιφορά} = 0.0199996874 \approx 0.02 kg \frac{m^2}{s^2}\] \[\frac{dL}{dt} = \frac{dL}{dt}_{spin} + \frac{dL}{dt}_{περιφορά} = 0.04 + 0.02 = 0.06 kg \frac{m^2}{s^2}\]Με όποιο τρόπο και να υπολογίσουμε το ρυθμό μεταβολής της στροφορμής μπορούμε να βρούμε την στροφορμή την συγκεκριμένη χρονική στιγμή αν γνωρίζουμε την αρχική στροφορμή
\[L_o = 0\]ως εξής
\[\frac{dL}{dt} = 0.06 \Rightarrow \frac{L - L_o}{Δt} = 0.06 \Rightarrow L = 0.6 kg \frac{m^2}{s}\]β’ τρόπος
Υπολογισμός της στιγμιαίας στροφορμής
\[L = L_{spin} + L_{περιστροφή} = Ι_{cm} \cdot ω + m \cdot u_{cm} \cdot r = \frac{1}{2} \cdot m \cdot R^2 \cdot ω + m \cdot u_{cm} \cdot \frac{R}{2} = 0.4 + 0.2 = 0.6 kg \frac{m^2}{s}\]blog comments powered by Disqus