Κρούση και ολίσθηση
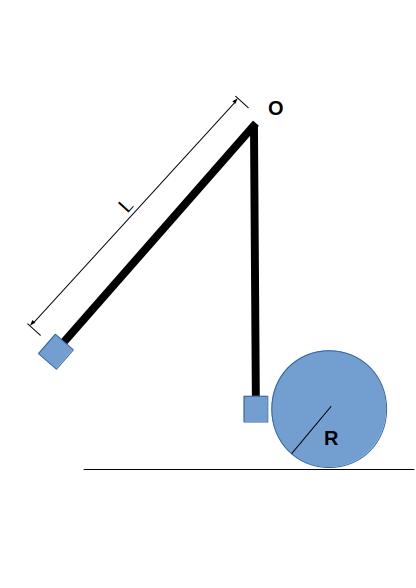
Λεπτή ομογενής και ισοπαχής ράβδος μάζας \(m\) και μήκους \(L=1.5m\), μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που περνά από το άκρο της O όπως φαίνεται στο σχήμα. Η ράβδος έχει στερεωμένο στο ένα της άκρο σώμα \(Σ_1\) μάζας \(m_1 = \frac{m}{2}\) αμελητέων διαστάσεων. Η ροπή αδράνειας της ράβδου γύρω από άξονα περιστροφής που περνάει από το κέντρο μάζας της και είναι κάθετος στο μήκος της ράβδου δίνεται από την σχέση \(I_ρ = \frac{1}{12} \cdot m \cdot L^2\). Η ράβδος αρχικά ισορροπεί οριζόντια και αφήνεται να κινηθεί ελεύθερα, υπό την επίδραση μόνο της βαρύτητας. Όταν περνά από την κατακόρυφη θέση, το άκρο στο οποίο βρίσκεται το σώμα \(Σ_1\) συγκρούεται με αρχικά ακίνητη κοίλη σφαίρα μάζας \(m_2 = \frac{m}{4}\) και ακτίνας \(R= \frac{5}{8}m\) που βρίσκεται στο επίπεδο κίνησης της ράβδου όπως φαίνεται στο σχήμα. Αμέσως μετά την κρούση η κοίλη σφαίρα αποκτά μόνο μεταφορική ταχύτητα, ενώ η γωνιακή ταχύτητα της ράβδου έχει μέτρο \(ω_1 =1 \frac{rad}{s}\) και κατεύθυνση αντίθετη με αυτήν που είχε πριν την κρούση. Αν ο συντελεστής τριβής ολίσθησης μεταξύ της κοίλης σφαίρας και του εδάφους είναι \(μ=0.1\) να βρεθεί το διάστημα που διανύει η κοίλη σφαίρα σε χρόνο \(Δt=12s\) αμέσως μετά την σύγκρουση. Οι αντιστάσεις από τον αέρα θεωρούνται αμελητέες. Δίνεται επίσης η ροπή αδράνειας της κοίλης σφαίρας \(I = \frac{2}{3} \cdot m_2 \cdot R^2\), και η επιτάχυνση της βαρύτητας \(g=10 \frac{m}{s^2}\).
Απάντηση:
Για την κίνηση της ράβδου εφαρμόζουμε την αρχή διατήρησης της μηχανικής ενέργειας:
\[Κ_Ι + U_I = K_{II} + U_{II} \Rightarrow 0 + (m + m_1) \cdot g \cdot L = \frac{1}{2} \cdot I \cdot ω^2 + m \cdot g \cdot \frac{L}{2}\]και κάνοντας αντικαταστάσεις και πράξεις υπολογίζουμε την γωνιακή ταχύτητα της ράβδου στην κατακόρυφη θέση \(ω = 4 \frac{rad}{s}\)
Για την κρούση του συστήματος ράβδος - σώμα \(Σ_1\) με την ακίνητη κοίλη σφαίρα ισχύει η αρχή διατήρησης της στροφορμής:
\[L_{πριν} = L_{μετά} \Rightarrow I \cdot ω = -Ι \cdot ω_1 + m_2 \cdot υ_ο \cdot L\]οπότε μετά τις αντικαταστάσεις έχουμε \(υ_ο = 25 \frac{m}{s}\).
H κοίλη σφαίρα κάνει σύνθετη κίνηση (μεταφορική και περιστροφική). Η μεταφορική κίνηση είναι ευθύγραμμη ομαλά επιβραδυνόμενη εξαιτίας της τριβής ολίσθησης, ενώ η περιστροφική είναι κυκλική ομαλά επιταχυνόμενη εξαιτίας της ροπής της τριβής ολίσθησης.
\[ΣF = m \cdot α_{cm} \Rightarrow μ \cdot m_2 \cdot g = m_2 \cdot α_{cm}\]από όπου υπολογίζουμε την επιβράδυνση \(α_{cm} = 1 \frac{m}{s^2}\)
\[Στ = Ι \cdot α_{γων} \Rightarrow T \cdot R = \frac{2}{3} \cdot m_2 \cdot R^2 \cdot α_{γων}\]και κάνοντας πράξεις έχουμε \(α_{γων} = 2.4 \frac{rad}{s^2}\)
καθώς ελαττώνεται η \(υ_{cm}\) και ταυτόχρονα αυξάνεται η \(ω\) κάποια στιγμή ξεκινάει η κοίλη σφαίρα να κυλίεται, όταν
\[υ_{cm} = ω \cdot R \Rightarrow υ_ο - α_{cm} \cdot t = α_{γων} \cdot t \cdot R \Rightarrow t = 10s\]Άρα η ολίσθηση διαρκεί \(t_1 = 10s\), ενώ τον υπόλοιπο χρόνο \(t_2 = t - t_1 = 2s\) η κοίλη σφαίρα κυλίεται με ταχύτητα
\[υ_{cm} = υ_ο - α_{cm} \cdot t = 15 \frac{m}{s}\]To διάστημα που διανύει η κοίλη σφαίρα καθώς ολισθαίνει δίνεται από την σχέση
\[x_{1cm} = υ_ο \cdot t_1 - \frac{1}{2} \cdot α_{cm} \cdot t_1^2 = 200m\]To διάστημα που διανύει η κοίλη σφαίρα καθώς κυλίεται δίνεται από την σχέση
\[x_{2cm} = υ_{cm} \cdot t_2 = 30m\]άρα το συνολικό διάστημα που διανύει η κοίλη σφαίρα μετά την σύγκρουση είναι:
\[s_{ολ} = 230m\]blog comments powered by Disqus