Σκάλα και ρυθμός μεταβολής
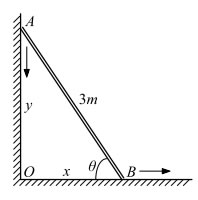
Μία σκάλα μήκους \(L = 3m\) είναι τοποθετημένη σ’ έναν τοίχο. Τη χρονική στιγμή \(t_0\) το κάτω μέρος της σκάλας γλιστράει στο δάπεδο με ρυθμό \(0.1 \frac{m}{s}\) και η κορυφή της σκάλας απέχει από το δάπεδο \(2.5m\). Γι αυτή την χρονική στιγμή να βρείτε:
i) Το ρυθμό μεταβολής της γωνίας \(θ\) (Σχήμα).
ii) Την ταχύτητα με την οποία πέφτει η κορυφή \(Α\) της σκάλας.
iii) Την επιτάχυνση του κέντρου μάζας αν θεωρήσετε τη σκάλα σαν μια ομογενή δοκό, για την οποία η ροπή αδράνειας, ως προς κάθετο άξονα που περνά από το μέσον της, δίνεται από τη σχέση \(Ι_{cm}= \frac{1}{12} \cdot Μ \cdot l^2\), ενώ η επιτάχυνση της βαρύτητας είναι \(g=10 \frac{m}{s^2}\).
Απάντηση:
Τα μεγέθη \(x, y, θ\) είναι συναρτήσεις του χρόνου, δηλαδή ισχύει \(x = x(t), y = y(t), θ = θ(t)\) και από τα δεδομένα έχουμε:
\[υ_Α(t_0) = \frac{dy(t_0)}{dt}\] \[υ_B(t_0) = \frac{dx(t_0)}{dt} = 0.1 \frac{m}{s}\]Τη χρονική στιγμή \(t_0\) , που η κορυφή της σκάλας απέχει από το δάπεδο \(2.5m\) είναι:
\[y(t_0) = 2.5m\]Όμως ισχύει το πυθαγόρειο θεώρημα για το ορθογώνιο τρίγωνο, οπότε:
\[x(t_0)^2 + y(t_0)^2 = L^2 \Rightarrow x(t_0) = \sqrt{3^2 - y(t_0)^2} \Rightarrow x(t_0) = \sqrt{2.75}m\] \[συνθ(t) = \frac{x(t)}{L} \Rightarrow x(t) = 3 \cdot συνθ(t) \Rightarrow \frac{dx}{dt} = - 3 \cdot ημθ(t) \cdot \frac{dθ}{dt}\] \[\frac{dθ}{dt} = - \frac{1}{3 \cdot ημθ(t)} \cdot \frac{dx}{dt} \Rightarrow \frac{dθ(t_0)}{dt} = - \frac{1}{3 \cdot ημθ(t_0)} \cdot \frac{dx(t_0)}{dt}\]και μετά τις αντικαταστάσεις αφού \(ημθ(t_0) = \frac{y(t_0)}{L} = \frac{2.5}{3}\)
\[\frac{dθ(t_o)}{dt} = - \frac{1}{25} \frac{rad}{s}\]Πάλι για το ορθογώνιο τρίγωνο έχουμε το πυθαγόρειο θεώρημα, σχέση που παραγωγίζουμε ως προς το χρόνο:
\[x(t)^2 + y(t)^2 = L^2 \Rightarrow 2 \cdot x(t) \cdot \frac{dx}{dt} + 2 \cdot y(t) \cdot \frac{dy}{dt} = 0 \Rightarrow \frac{dy}{dt} = - \frac{x(t)}{y(t)} \cdot \frac{dx}{dt}\]οπότε
\[\frac{dy(t_0)}{dt} = - \frac{x(t_0)}{y(t_0)} \cdot \frac{dx(t_0)}{dt}\]κα μετά τις αντικαταστάσεις
\[\frac{dy(t_o)}{dt} = - \frac{\sqrt{2.75}}{25} \frac{m}{s}\]Τα προηγούμενα αποτελούν την λύση της άσκησης 7 στην ενότητα 2.4 Ρυθμός μεταβολής, και υπάρχουν στο βιβλίο του οργανισμού Μαθηματικά Γ’ Γενικού Λυκείου, Θετική και Τεχνολογική Κατεύθυνση. Πέρα από την προσέγγιση των Μαθηματικών, υπάρχει όμως και η προσέγγιση της Φυσικής για τα πρώτα δύο ερωτήματα.
Η ράβδος λοιπόν εκτελεί σύνθετη κίνηση και μεταφορική και περιστροφική. Με τον ίδιο τρόπο κινούνται και τα άκρα της \(Α\) και \(Β\). Στο σχήμα που ακολουθεί έχουν σχεδιαστεί με κόκκινα διανύσματα οι ταχύτητες \(υ_{xcm}\) και \(υ_{ycm}\) των άκρων \(Α\) και \(Β\) λόγω της μεταφορικής κίνησης, ενώ με μπλε διανύσματα η γραμμική ταχύτητα \(υ_{γραμ}\) και οι συνιστώσες της στους άξονες \(υ_{xγραμ}\) και \(υ_{yγραμ}\)
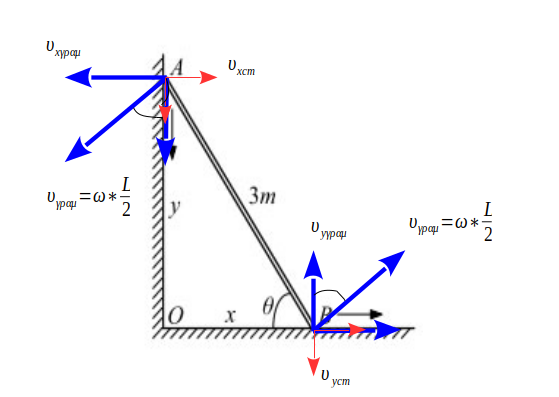
Για την γραμμική ταχύτητα γνωρίζουμε:
\[υ_{γραμ} = ω \cdot R \Rightarrow υ_{γραμ} = ω \cdot \frac{L}{2}\]ενώ οι συνιστώσες της υπολογίζονται ως εξής:
\[συνθ = \frac{υ_{yγραμ}}{υ_{γραμ}} \Rightarrow υ_{yγραμ} = ω \cdot \frac{L}{2} \cdot συνθ\] \[ημθ = \frac{υ_{xγραμ}}{υ_{γραμ}} \Rightarrow υ_{xγραμ} = ω \cdot \frac{L}{2} \cdot ημθ\]Λόγω της γεωμετρίας του προβλήματος, για όσο χρόνο η ράβδος είναι σε επαφή με τον κατακόρυφο τοίχο, η οριζόντια συνιστώσα της συνισταμένης ταχύτητας του άκρου \(Α\) της ράβδου είναι μηδέν, άρα ισχύει:
\[υ_{xcm} = ω \cdot \frac{L}{2} \cdot ημθ\] \[υ_Α = υ_{ycm} + ω \cdot \frac{L}{2} \cdot συνθ\]ενώ λόγω της γεωμετρίας για το άκρο \(Β\) της ράβδου η κατακόρυφος συνιστώσα της συνισταμένης ταχύτητας είναι μηδέν άρα ισχύει:
\[υ_{ycm} = ω \cdot \frac{L}{2} \cdot συνθ\] \[υ_Β = υ_{xcm} + ω \cdot \frac{L}{2} \cdot ημθ\]Έχουμε έτσι ένα σύστημα τεσσάρων εξισώσεων με τέσσερις αγνώστους τους \(υ_{xcm}, υ_{ycm}, ω, υ_Α\). Οπότε αντικαθιστώντας όπου \(L = 3m\), \(υ_Β = 0.1 \frac{m}{s}\), \(ημθ = \frac{2.5}{3}\) και \(συνθ = \frac{\sqrt{2.75}}{3}\) έχουμε:
\[υ_{xcm} = ω \cdot \frac{3}{2} \cdot \frac{2.5}{3} \Rightarrow υ_{xcm} = 1.25 \cdot ω\] \[υ_Α = υ_{ycm} + ω \cdot \frac{3}{2} \cdot \frac{\sqrt{2.75}}{3} \Rightarrow υ_Α = υ_{ycm} + \frac{\sqrt{2.75}}{2} \cdot ω\] \[υ_{ycm} = ω \cdot \frac{3}{2} \cdot \frac{\sqrt{2.75}}{3} \Rightarrow υ_{ycm} = \frac{\sqrt{2.75}}{2} \cdot ω\] \[υ_{xcm} + ω \cdot \frac{3}{2} \cdot \frac{2.5}{3} = 0.1 \Rightarrow υ_{xcm} + 1.25 \cdot ω = 0.1\]Η τελευταία εξίσωση γίνεται λόγω της πρώτης
\[1.25 \cdot ω + 1.25 \cdot ω = 0.1 \Rightarrow 2.5 \cdot ω = 0.1 \Rightarrow ω = \frac{1}{25} \frac{rad}{s}\]Αυτή είναι η απάντηση στο πρώτο ερώτημα, μιας και ο ρυθμός μεταβολής της γωνίας \(θ\) είναι η γωνιακή ταχύτητα \(ω\). Για την ακρίβεια έχει υπολογιστεί το μέτρο της γωνιακής ταχύτητας. Το πρόσημο \(-\) που εμφανίστηκε στην προηγούμενη λύση δηλώνει το γεγονός ότι η γωνία μικραίνει. Με γνωστό το \(ω\) μπορούμε να υπολογίσουμε και τα υπόλοιπα:
\[υ_{xcm} = 1.25 \cdot \frac{1}{25} = 0.03 \frac{m}{s}\] \[υ_{ycm} = \frac{\sqrt{2.75}}{2} \cdot \frac{1}{25} = \frac{\sqrt{2.75}}{50} \frac{m}{s}\] \[υ_Α = \frac{\sqrt{2.75}}{50} + \frac{\sqrt{2.75}}{2} \cdot \frac{1}{25} = \frac{\sqrt{2.75}}{25} \frac{m}{s}\]Πάλι το πρόσημο \(-\) που εμφανίστηκε στην προηγούμενη λύση μας δίνει την κατεύθυνση της ταχύτητας του άκρου \(Α\), που είναι προς την αρχή του άξονα των συντεταγμένων. Εδώ υπολογίστηκε το μέτρο της ταχύτητας του άκρου \(Α\).
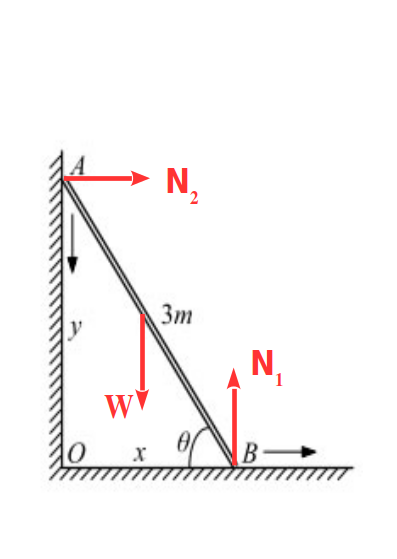
Εάν η ράβδος είναι το σύστημά μας, τότε το περιβάλλον αποτελούν η γη, ο οριζόντιος και ο κατακόρυφος τοίχος. Οι δυνάμεις που ασκούνται έτσι στη ράβδο είναι το βάρος της που ασκείται στο κέντρο μάζας της, η κάθετη αντίδραση \(Ν_1\) που ασκείται από τον οριζόντιο τοίχο στο άκρο \(Β\) και η κάθετη αντίδραση \(Ν_2\) που ασκείται από τον κατακόρυφο τοίχο στο άκρο \(Α\). (Θεωρούμε ότι δεν υπάρχει τριβή μεταξύ της ράβδου και των τοίχων).
Εφαρμόζουμε τον δεύτερο νόμο του Νεύτωνα για τον άξονα \(x\)
\[ΣF_x = m \cdot α_{xcm} \Rightarrow N_2 = m \cdot α_{xcm}\]και δεύτερος νόμος του Νεύτωνα για τον άξονα \(y\)
\[ΣF_y = m \cdot α_{ycm} \Rightarrow m \cdot g - N_1 = m \cdot α_{ycm}\]η ράβδος εκτός από την μεταφορική κίνηση εκτελεί και περιστροφική γύρω από άξονα που διέρχεται από το κέντρο μάζας της. Έτσι το αλγεβρικό άθροισμα των ροπών ως προς άξονα που διέρχεται από το κέντρο μάζας της ράβδου είναι
\[Στ = Ι \cdot α_{γων} \Rightarrow τ_{Ν_1} - τ_{Ν_2} = \frac{1}{12} \cdot m \cdot L^2 \cdot α_{γων} \Rightarrow N_1 \cdot \frac{L}{2} \cdot συνθ - Ν_2 \cdot \frac{L}{2} \cdot ημθ = \frac{1}{12} \cdot m \cdot L^2 \cdot α_{γων}\]μέχρι στιγμής έχουμε τρεις εξισώσεις με πέντε αγνώστους τους \(Ν_1, Ν_2, α_{γων}, α_{xcm}, α_{ycm}\). Και η μάζα είναι άγνωστη αλλά στη συνέχεια θα απλοποιηθεί. Οι δύο εξισώσεις που απομένει να γράψουμε για να φτάσουμε σε ένα σύστημα πέντε εξισώσεων με πέντε αγνώστους, προέρχονται από τις κινήσεις που εκτελούν τα άκρα \(Α\) και \(Β\) της ράβδου. Το άκρο \(Α\) όπως και όλη η ράβδος κάνει σύνθετη κίνηση και μεταφορική και περιστροφική. Έτσι εκτός των επιταχύνσεων \(α_{xcm}\) και \(α_{ycm}\) που αφορούν τη μεταφορική κίνηση έχει και την επιτρόχια επιτάχυνση \(α_{επιτ}\) που αφορά στην περιστροφική κίνηση του άκρου \(Α\) γύρω από το κέντρο μάζας της ράβδου. Στο επόμενο σχήμα έχουμε αναλύσει αυτή την επιτάχυνση στους άξονες \(x\) και \(y\) (μπλε διανύσματα), ενώ φαίνονται και τα διανύσματα \(α_{xcm}\) και \(α_{ycm}\) (κόκκινα διανύσματα).
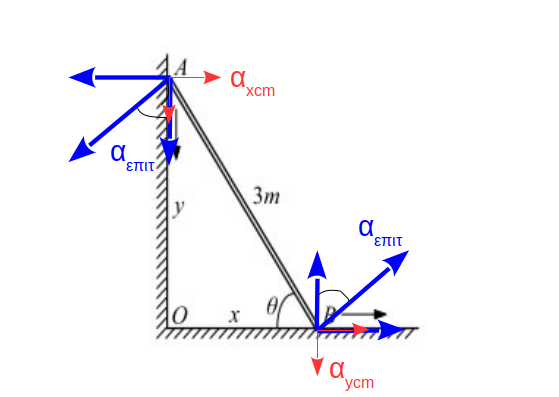
Έστω \(α_{xεπιτ}\) η οριζόντια συνιστώσα της επιτρόχιας επιτάχυνσης για την οποία ισχύει:
\[α_{xεπιτ} = α_{επιτ} \cdot ημθ \Rightarrow α_{xεπιτ} = α_{γων} \cdot \frac{L}{2} \cdot ημθ\]Επειδή η κίνηση του άκρου \(Α\) είναι επιταχυνόμενη κατακόρυφη κίνηση βγάζουμε το συμπέρασμα ότι η συνολική οριζόντια επιτάχυνση για το άκρο \(Α\) θα πρέπει να είναι μηδέν, δηλαδή:
\[α_{γων} \cdot \frac{L}{2} \cdot ημθ = α_{xcm}\]Ανάλογα ισχύουν και για την κίνηση του άκρου \(Β\) της ράβδου, μόνο που λόγω της επιταχυνόμενης οριζόντιας κίνησής του βγάζουμε το συμπέρασμα ότι η συνολική κατακόρυφη επιτάχυνσή του θα πρέπει να είναι μηδέν, δηλαδή:
\[α_{γων} \cdot \frac{L}{2} \cdot συνθ = α_{ycm}\]Έτσι έχουμε να λύσουμε το παρακάτω σύστημα πέντε εξισώσεων με πέντε αγνώστους
\[N_2 = m \cdot α_{xcm}\] \[m \cdot g - N_1 = m \cdot α_{ycm}\] \[N_1 \cdot \frac{L}{2} \cdot συνθ - Ν_2 \cdot \frac{L}{2} \cdot ημθ = \frac{1}{12} \cdot m \cdot L^2 \cdot α_{γων}\] \[α_{γων} \cdot \frac{L}{2} \cdot ημθ = α_{xcm}\] \[α_{γων} \cdot \frac{L}{2} \cdot συνθ = α_{ycm}\]όπου \(L = 3m\), \(ημθ = \frac{2.5}{3}\) και \(συνθ = \frac{\sqrt{2.75}}{3}\)
Θα λύσουμε τις πρώτες δύο εξισώσεις ως προς \(Ν_1\) και \(Ν_2\)
\[Ν_1 = m \cdot g - m \cdot α_{ycm}\] \[N_2 = m \cdot α_{xcm}\]και αντικαθιστώντας στην 3η τα \(Ν_1, Ν_2, α_{ycm}, α_{xcm}\) ο μόνος άγνωστος είναι η \(α_{γων}\).
και κάνοντας πράξεις, αφού χρησιμοποιήσουμε και την ταυτότητα \(ημ^2θ+συν^2θ = 1\) έχουμε:
\[α_{γων} = \frac{5}{3} \cdot \sqrt{2.75} \frac{rad}{s^2}\]οπότε εύκολα υπολογίζουμε τις \(α_{xcm}\) και \(α_{ycm}\)
\[α_{xcm} = \frac{12.5 \sqrt{2.75}}{6} \frac{m}{s^2}\] \[α_{ycm} = \frac{13.75}{6} \frac{m}{s^2}\]και τελικά η συνισταμένη των \(α_{xcm}\) και \(α_{ycm}\) είναι:
\[α_{cm} = \sqrt{α_{xcm}^2 + α_{ycm}^2} \Rightarrow α_{cm} = 2.5 \cdot \sqrt{2.75} \frac{m}{s^2}\]Σχετική βιβλιογραφία:
Variations of the Sliding Ladder Problem, Stelios Kapranidis and Reginald Koo
The Falling Ladder Paradox, Paul Scholten, Andrew Simoson
Sliding ladder, Physics Harvard Education, Solution Week 47 (8/4/03)
Dynamics of a sliding ladder leaning against a wall J B Oliveira, at all
blog comments powered by Disqus