Πανελλήνιες 2011 Θέμα Δ1
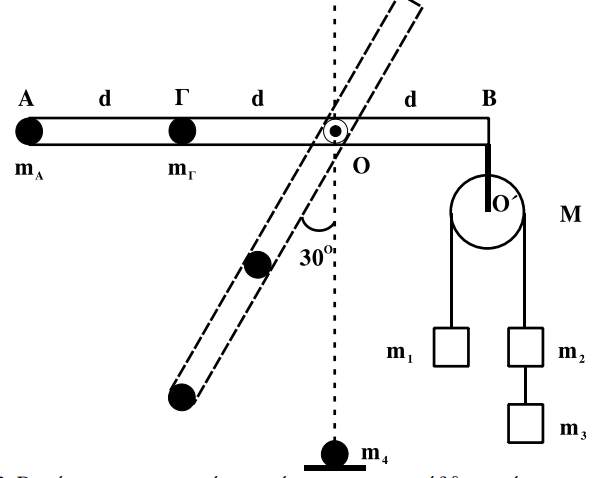
Αβαρής ράβδος μήκους \(3 \cdot d\) με \((d=1m)\) μπορεί να στρέφεται γύρω από οριζόντιο άξονα, που είναι κάθετος σε αυτήν και διέρχεται από το \(Ο\). Στο άκρο \(Α\) που βρίσκεται σε απόσταση \(2 \cdot d\) από το \(Ο\) υπάρχει σημειακή μάζα \(m_A = 1kg\) και στο σημείο \(Γ\), που βρίσκεται σε απόσταση \(d\) από το \(Ο\) έχουμε επίσης σημειακή μάζα \(m_Γ = 6kg\). Στο άλλο άκρο της ράβδου, στο σημείο \(Β\), είναι αναρτημένη τροχαλία μάζας \(Μ = 4kg\) από την οποία κρέμονται οι μάζες \(m_1 = 2kg\), \(m_2 = m_3 = 1kg\). Η τροχαλία μπορεί να περιστρέφεται γύρω από άξονα \(Ο\). Αποδείξτε ότι το σύστημα ισορροπεί με τη ράβδο στην οριζόντια θέση.
Θεωρούμε τα νήματα αβαρή, μη εκτατά και τεντωμένα. Λέγοντας ότι το σύστημα ισορροπεί εννοούμε ότι το σύστημα είναι ακίνητο αν ήταν αρχικά ακίνητο ή περιστρέφεται με σταθερή γωνιακή ταχύτητα αν αρχικά περιστρέφονταν με αρχική γωνιακή ταχύτητα. Θα αποδείξουμε ότι το σύστημα ισορροπεί με τη ράβδο στην οριζόντια θέση. (Δυστυχώς το σύστημα ισορροπεί με τη ράβδο σε οποιαδήποτε θέση, αλλά αυτό είναι αστοχία της άσκησης) Το σύστημα αποτελείται από πέντε ξεχωριστά σώματα: Την ράβδο, την τροχαλία και τις τρεις μάζες \(\quad m_1, \quad m_2, \quad m_3\)
Για την ράβδο περιβάλλον αποτελούν η γη, ο άξονας περιστροφής και το νήμα που την συνδέει με την τροχαλία. Στο σχήμα φαίνονται οι δυνάμεις που ασκεί το περιβάλλον στην ράβδο.
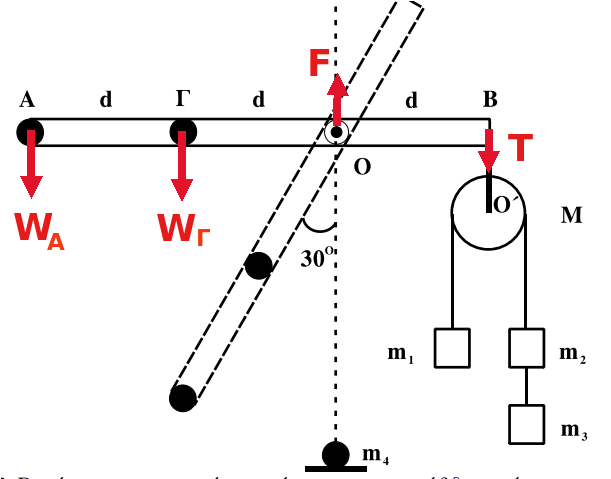
Θεωρούμε ότι την στιγμή που αφήνουμε ελεύθερη την ράβδο στην οριζόντια θέση, αυτή θα περιστραφεί με γωνιακή επιτάχυνση \(α_{γων}\) με θετική την φορά που είναι αντίθετη της φοράς περιστροφής των δεικτών του ρολογιού.
\[Σ\vec{τ_Ο} = Ι \cdot \vec{α}_{γων} \Rightarrow W_A \cdot 2d + W_Γ \cdot d - T \cdot d = I \cdot α_{γων}\] \[Ι = Ι_Α + Ι_Γ \Rightarrow Ι = m_A \cdot (2d)^2 + m_Γ \cdot d^2\]H επιτάχυνση του κέντρου μάζας της τροχαλίας εφόσον το νήμα είναι μη εκτατό είναι ταυτόχρονα και γραμμική επιτάχυνση του άκρου \(Β\) της ράβδου.
\[α_B = α_{γων} \cdot d \Rightarrow α_{cm} = α_{γων} \cdot d \Rightarrow α_{γων} = \frac{α_{cm}}{d}\]Χρησιμοποιώντας τις προηγούμενες σχέσεις και κάνοντας τις πράξεις φτάνουμε στην πρώτη εξίσωση.
\[2m_A \cdot g + m_Γ \cdot g - T = (4m_A + m_Γ)\cdot α_{cm}\]Για την τροχαλία περιβάλλον αποτελούν η γη και τα τρία νήματα που την συνδέουν με την ράβδο και τα σώματα μάζας \(m_1\) και \(m_2\). Στο σχήμα φαίνονται οι δυνάμεις που ασκεί το περιβάλλον στην ράβδο.
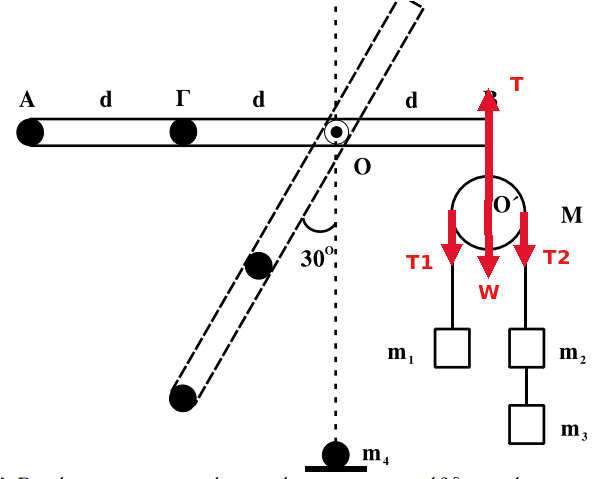
H τροχαλία δεν περιστρέφεται γύρω από το κέντρο της \(Ο\) και αυτό το γνωρίζουμε διότι ισχύει
\[m_1 = m_2 + m_3\]Αν δηλαδή υπολογίσουμε την συνολική ροπή ως προς άξονα που διέρχεται από το \(Ο'\) έχουμε:
\[Στ_Ο' = T_1 \cdot R - T_2 \cdot R \Rightarrow Στ_Ο' = m_1 \cdot g \cdot R - (m_2 + m_3) \cdot g \cdot R \Rightarrow Στ_Ο' =0\]Συνέπεια αυτής της μη περιστροφής είναι ότι όλα τα σημεία της τροχαλίας εκτελούν μεταφορική κίνηση με επιτάχυνση την επιτάχυνση του κέντρου μάζας της, άρα και τα σημεία που τα νήματα ακουμπούν στην τροχαλία και αυτό πάλι έχει σαν συνέπεια ότι οι επιταχύνσεις των μαζών \(m_1\) και \(m_2\) άρα και \(m_3\) είναι και αυτές ίσες με την επιτάχυνση \(α_{cm}\)
Για το σώμα μάζας \(m_1\) περιβάλλον αποτελούν η γη και το νήμα που το συνδέει με την τροχαλία. Στο σχήμα φαίνονται οι δυνάμεις που ασκεί το περιβάλλον στο σώμα μάζας \(m_1\)
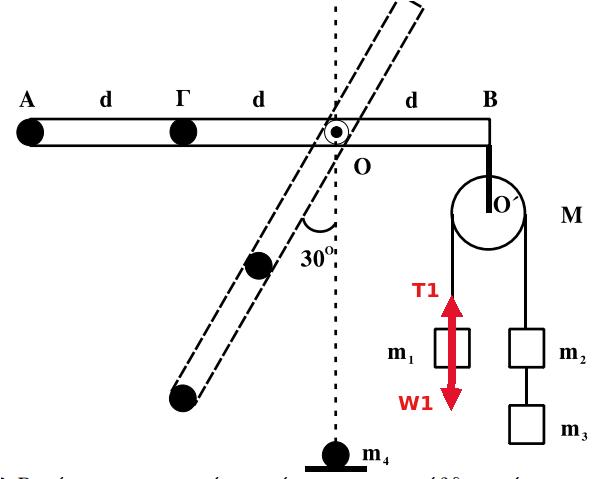
Για το σώμα μάζας \(m_2\) περιβάλλον αποτελούν η γη και τα νήματα που το συνδέουν με την τροχαλία και το σώμα μάζας \(m_3\). Στο σχήμα φαίνονται οι δυνάμεις που ασκεί το περιβάλλον στο σώμα μάζας \(m_2\)
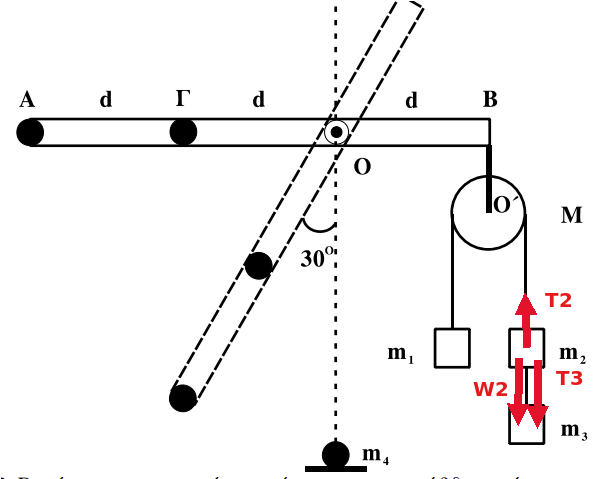
Για το σώμα μάζας \(m_3\) περιβάλλον αποτελούν η γη και το νήμα που το συνδέει με το σώμα μάζας \(m_2\). Στο σχήμα φαίνονται οι δυνάμεις που ασκεί το περιβάλλον στο σώμα μάζας \(m_3\)
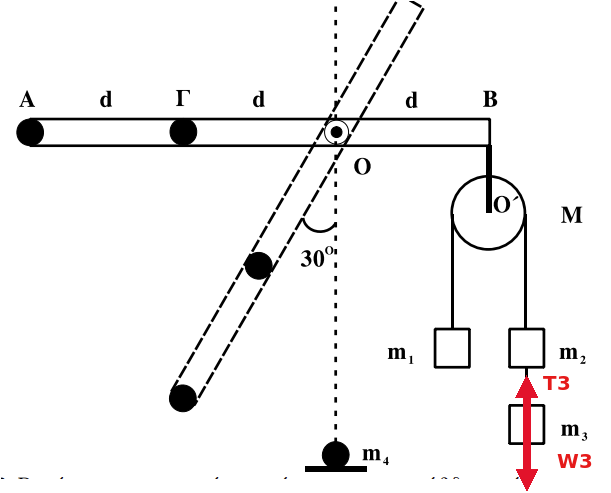
Έχουμε να λύσουμε ένα σύστημα \(5\) εξισώσεων με \(5\) αγνώστους τους \(\quad Τ, \quad Τ_1, \quad Τ_2, \quad T_3, \quad α_{cm} \quad\) Μετά τη λύση του συστήματος έχουμε
\[α_{cm} = 0 \Rightarrow α_{γων} = 0 \Rightarrow Σ\vec{τ_Ο} = 0\]H συνηθισμένη λύση!
Στο σημείο \(Β\) ασκείται δύναμη τάσης \(Τ\) ίση με το συνολικό βάρος του συστήματος τροχαλίας - \(m_1, \quad m_2, \quad m_3\) αφού το σύστημα ισορροπεί.
\[Τ = M \cdot g + m_1 \cdot g + m_2 \cdot g + m_3 \cdot g \Rightarrow T = 80 N\]Στην οριζόντια θέση για την τροχαλία ισχύει:
\[Στ = m_A \cdot g \cdot 2d + m_Γ \cdot g \cdot d - T \cdot d = 0 Nm\] \[Σ\vec{τ_Ο} = Ι \cdot \vec{α}_{γων} \Rightarrow α_{γων} =0\]άρα το σύστημα ισορροπεί με την ράβδο στην οριζόντια θέση!
η συνηθισμένη λύση εδώ μετά το 8:00.
Μπορείτε να εκτυπώσετε τα θέματα από εδώ
blog comments powered by Disqus