Η δύναμη του ελατηρίου
Σώμα μάζας \(m\) ισορροπεί δεμένo στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \(k\), του οποίου το κάτω άκρο είναι στερεωμένο στο δάπεδο. Ανεβάζουμε το σώμα κατακόρυφα προς τα πάνω κατά \(d = 2\frac{m \cdot g}{k}\) και το αφήνουμε ελεύθερο οπότε αυτό εκτελεί απλή αρμονική ταλάντωση. Θέλουμε να γράψουμε την εξίσωση της δύναμης του ελατηρίου που ασκείται στο σώμα σε συνάρτηση με την απομάκρυνση \(x\) από τη θέση ισορροπίας \(Ο\) της ταλάντωσης. Δίνεται η επιτάχυνση της βαρύτητας \(g\) και θετική φορά η προς τα πάνω.
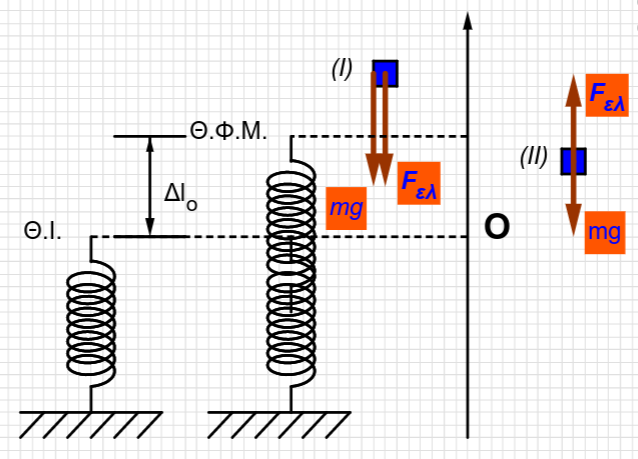
Θέση ισορροπίας
\[ΣF=0 \Rightarrow F_{ελ}-W=0 \Rightarrow k\cdot Δl_0=m\cdot g \Rightarrow Δl_0 = \frac{m \cdot g}{k}\]Τυχαία θέση \(Ι\)
\[\frac{mg}{k} \leq x \leq 2\frac{mg}{k}\]α) τρόπος
\[F_{ελ} = -k \cdot Δl \Rightarrow F_{ελ} = -k(x-Δl_0) \Rightarrow F_{ελ} = -k \cdot x + m\cdot g\]το αρνητικό πρόσημο δείχνει ότι η φορά της δύναμης του ελατηρίου είναι προς τα κάτω.
β) τρόπος
\[ΣF = -D \cdot x \Rightarrow F_{ελ} - m\cdot g = - k\cdot x \Rightarrow F_{ελ} = -k \cdot x + m \cdot g\]θεωρούμε την αλγεβρική τιμή της \(F_{ελ}\) θετική, αφού οι πράξεις θα μας δώσουν το πρόσημό της, άρα θα γνωρίζουμε και μέτρο και κατεύθυνση.
Τυχαία θέση \(IΙ\)
\[0\leq x \leq \frac{mg}{k}\]α) τρόπος
\[F_{ελ} = k \cdot Δl \Rightarrow F_{ελ} = k(Δl_0-x) \Rightarrow F_{ελ} = -k \cdot x + m\cdot g\]το θετικό πρόσημο δείχνει ότι η φορά της δύναμης του ελατηρίου είναι προς τα πάνω.
β) τρόπος
\[ΣF = -D \cdot x \Rightarrow F_{ελ} - m\cdot g = - k\cdot x \Rightarrow F_{ελ} = -k \cdot x + m \cdot g\]blog comments powered by Disqus