Επαναληπτικές εξετάσεις 2020
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(β\)
Α3 - \(δ\)
Α4 - \(γ\)
Α5: \(Σ - Σ - Λ - Λ - Λ\)
Θέμα Β
B1-\((ii)-2-7\)
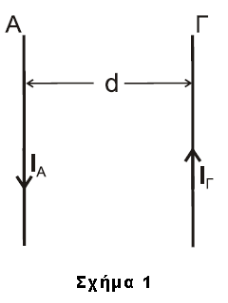
άρα σωστό το ii)
B2-\((iii)-2-6\)
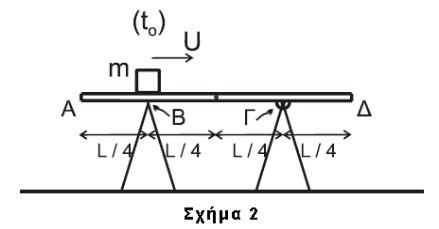
άρα σωστό το iii)
B3-\((i)-2-6\)
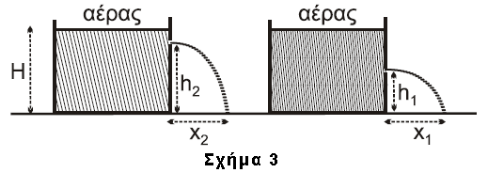
άρα σωστό το \(i\)
Θέμα Γ
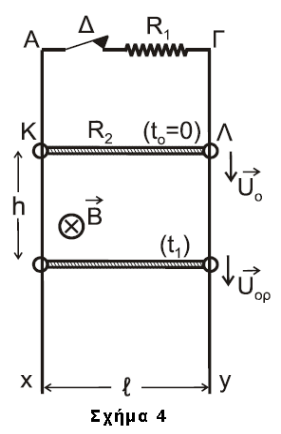
Γ1-\((5)\)
\[Ε_{επ} = \frac{ΔΦ}{Δt} = \frac{B \cdot ΔS}{Δt} = \frac{B \cdot l \cdot Δx}{Δt} = B \cdot l \cdot υ\] \[Ε_{επ}^{(ο)} = Β \cdot υ_ο \cdot l \Rightarrow E_{επ} = 24 V\] \[I_o = \frac{E_{επ}}{R_{ολ}} = \frac{B \cdot l \cdot υ_ο}{R_1 + R_2} = 3 A\] \[F_L = B \cdot I \cdot l \Rightarrow F_L = 6N\] \[α = \frac{ΣF}{m} = \frac{m \cdot g - F_L}{m} = -20 \frac{m}{s^2}\]Γ2-\((5)\)
\[α = 0 \Rightarrow ΣF = 0 \Rightarrow F_L = m \cdot g\] \[B \cdot I_{επ} \cdot l = m\cdot g \Rightarrow I_{επ} = \frac{m \cdot g}{B \cdot l} = 1A\] \[E_{επ} = Ι_{επ} \cdot (R_1 +R_2) = 8 V\] \[υ_{ορ} = \frac{E_{επ}}{Β \cdot l} \Rightarrow υ_{ορ} = 4 \frac{m}{s}\]Γ3-\((8)\)
\[0 - t_1 : \quad q = \frac{ΔΦ}{R_{ολ}} \Rightarrow q = \frac{B \cdot l \cdot h}{R_1 + R_2}\] \[h = \frac{q \cdot (R_1 + R_2)}{B \cdot l} \Rightarrow h = 1.6 m\] \[Θ.Μ.Κ.Ε. \quad (0 \rightarrow h) \quad ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_B + W_{F_L}\] \[\frac{1}{2} \cdot m \cdot υ^2_{ορ} - \frac{1}{2} \cdot m \cdot υ^2_{ο} = m \cdot g \cdot h + W_{F_L} \Rightarrow W_{F_L} = -16J\] \[Q_1 + Q_2 = 16J\] \[Q_1 = \sum I^2_{επ} \cdot R_1 \cdot Δt\] \[Q_2 = \sum I^2_{επ} \cdot R_2 \cdot Δt\] \[\frac{Q_1}{Q_2} = \frac{R_1}{R_2} = \frac{1}{4}\] \[Q_1 = 4J, \quad Q_2 = 12J\]Γ4-\((7)\)
\[h_1 = υ_{ορ} \cdot Δt + \frac{1}{2} \cdot g \cdot Δt^2 \Rightarrow 0.45 = 4 \cdot Δt + 5 \cdot Δt^2\]και απορρίπτοντας την αρνητική ρίζα έχουμε \(Δt = 0.1s\)
\[υ = υ_{ορ} + g \cdot Δt \Rightarrow υ = 5 \frac{m}{s}\] \[\frac{dK}{dt} = \frac{dW}{dt} = \frac{ΣF \cdot dx}{dt} = ΣF \cdot υ\] \[\frac{dK}{dt} = 10 \frac{J}{s}\]Θέμα Δ
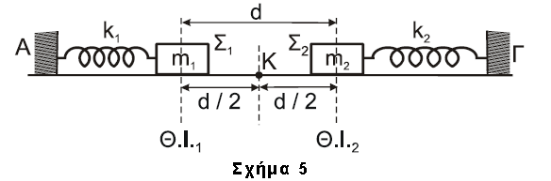
Δ1-\((4)\)
\[Τ_1 = 2 \cdot π \cdot \sqrt{\frac{m_1}{k_1}} = \frac{π}{2} s\] \[Τ_2 = 2 \cdot π \cdot \sqrt{\frac{m_2}{k_2}} = \frac{4π}{8} s\]Δ2-\((5)\)
\[ω_1 = \sqrt{\frac{k_1}{m_1}} = 4 \frac{rad}{s}\] \[ω_2 = \sqrt{\frac{k_2}{m_2}} = 5 \frac{rad}{s}\] \[x_1 = A \cdot ημ(ωt + φ_ο) \Rightarrow -0.6 = 0.6 \cdot ημ(4t + φ_ο)\] \[φ_ο = \frac{3 \cdot π}{2} rad\] \[x_1 = 0.6 \cdot ημ(4t + \frac{3 \cdot π}{2}) \quad S.I.\] \[υ_1 = 2,4 \cdot συν(4t + \frac{3 \cdot π}{2}) \quad S.I.\]ομοίως
\[x_2 = 0.6 + 0.2 \cdot \sqrt3 \cdot ημ(5t + \frac{π}{2}) \quad S.I.\] \[υ_2 = \sqrt3 συν(5t + \frac{π}{2}) \quad S.I.\]Δ3-\((6)\)
\[x_1 = \frac{d}{2} = 0.3 m\] \[0.3 = 0.6 \cdot ημ(4t + \frac{3 \cdot π}{2}) \Rightarrow t = \frac{π}{6} s\] \[x_2 = \frac{d}{2} = 0.3 m\] \[0.3 = 0.6 + 0.2 \sqrt3 \cdot ημ(5t + \frac{π}{2}) \Rightarrow t = \frac{π}{6} s\]άρα συγκρούονται στο μέσον αφού για \(t = \frac{π}{6} s \Rightarrow x_1 = x_2 = 0.3 m\)
Δ4-\((7)\)
\[t = \frac{π}{6} s\] \[υ_1 = 2,4 \cdot συν(\frac{4 \cdot π}{6} + \frac{3 \cdot π}{2}) = 1.2 \sqrt3 \frac{m}{s}\] \[υ_2 = \sqrt3 συν(\frac{5 \cdot π}{6} + \frac{π}{2}) = -0.5 \sqrt3 \frac{m}{s}\] \[υ'_1 = \frac{2 \cdot m_2}{m_1+m_2} \cdot υ_2 + \frac{m_1-m_2}{m_1+m_2} \cdot υ_1 = -1.2 \sqrt3 \frac{m}{s}\] \[υ'_2 = \frac{2 \cdot m1}{m_1+m_2} \cdot υ_1 + \frac{m_2-m_1}{m_1+m_2} \cdot υ_2 = 0.5 \sqrt3 \frac{m}{s}\]Δ5-\((3)\)
\[E_{ταλ} = Κ_1 + U_1 \Rightarrow \frac{1}{2} \cdot k_1 \cdot A^2_1 = \frac{1}{2} \cdot m_1 \cdot υ^2_1 + \frac{1}{2} \cdot k_1 \cdot x^2_1\]και μετά τις πράξεις \(A_1 = 0.6m\)
\[E_{ταλ} = Κ_2 + U_2 \Rightarrow \frac{1}{2} \cdot k_1 \cdot A^2_2 = \frac{1}{2} \cdot m_2 \cdot υ^2_2 + \frac{1}{2} \cdot k_2 \cdot x^2_2\]και μετά τις πράξεις \(A_2 = 0.2 \sqrt3 m\)
την χρονική στιγμή \(t_o = 0.6s, \quad x_1 = 0.3m, \quad υ_1<0\)
\[x_1 = 0.6 \cdot ημ(4(t-0.6) + \frac{5 \cdot π}{6}) \quad S.I.\] \[x_2 = 0.2 \cdot \sqrt3 \cdot ημ(5(t-0.6) + \frac{5π}{6}) \quad S.I.\]Για \(x_1 = 0.3m \Rightarrow t = 0.6 + \frac{π}{3}s\)
και για \(x_2 = 0.3m \Rightarrow t = 0.6 + \frac{π}{3}s\)
άρα συγκρούονται στο μέσον.
Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus