Φθίνουσα ταλάντωση και Πανεπιστήμιο
Φθίνουσα ταλάντωση
Στα περισσότερα πραγματικά συστήματα η κίνησή τους επιβραδύνεται από μη συντηρητικές δυνάμεις. Εμείς στο Λύκειο μελετάμε δύο περιπτώσεις τέτοιων δυνάμεων την Τριβή και την Αντίσταση του αέρα. Σε αυτά τα συστήματα η μηχανική ενέργεια μειώνεται ως προς τον χρόνο και η κίνηση λέμε ότι είναι φθίνουσα ή αποσβεννύμενη ταλάντωση.
Στην φθίνουσα ταλάντωση εκτός από την δύναμη επαναφοράς
\[F = -D \cdot x\]που εφαρμόζεται στο υλικό σημείο μπορεί να ασκείται και η δύναμη απόσβεσης
\[F' = - b \cdot υ\]Τέτοια δύναμη είναι η δύναμη αντίστασης που ασκείται σε μικρά αντικείμενα που κινούνται μέσα στον αέρα ή μέσα σε υγρό. Το b ονομάζεται σταθερά απόσβεσης και εξαρτάται από:
α) τις ιδιότητες του μέσου
β) το σχήμα του αντικειμένου
γ) το μέγεθος του αντικειμένου.
Κάνοντας χρήση του 2ου νόμου του Νεύτωνα έχουμε:
\[ΣF = m \cdot α \Rightarrow F + F' = m \cdot a\]και κάνοντας αντικατάσταση έχουμε:
\[-D \cdot x - b \cdot υ = m \cdot \frac{d^2x}{dt^2} \Rightarrow m \cdot \frac{d^2x}{dt^2} + D \cdot x + b \cdot υ =0\]Διαιρούμε με την μάζα και προκύπτει η παρακάτω διαφορική εξίσωση που είναι μια γραμμική ομογενής 2ας τάξης.
\[\frac{d^2x}{dt^2} + \frac{b}{m} \cdot \frac{dx}{dt} + \frac{D}{m} \cdot x = 0\]H σταθερά που εξαρτάται από την σταθερά απόσβεσης και τη μάζα του ταλαντούμενου σώματος συμβολίζεται με Λ και ονομάζεται εκθέτης απόσβεσης \(Λ = \frac{b}{2m}\). Εάν αντικαταστήσουμε τον λόγο \(\frac{D}{m}\) με το τετράγωνο της ιδιοσυχνότητας του συστήματος δηλαδή το \(ω_ο^2\) έχουμε:
\[\frac{d^2x}{dt^2} + 2 \cdot Λ \cdot \frac{dx}{dt} + ω_ο^2 \cdot x = 0\]Οι λύσεις της παραπάνω διαφορικής εξίσωσης είναι τρεις τελείως διαφορετικές συναρτήσεις που προκύπτουν ανάλογα με την σχέση που υπάρχει μεταξύ των παραμέτρων \(D, b, m\).
Όταν ισχύει \(Λ > ω_ο \Rightarrow b^2 > 4 \cdot D \cdot m\) έχουμε ισχυρή απόσβεση.
Όταν ισχύει \(Λ = ω_ο \Rightarrow b^2 = 4 \cdot D \cdot m\) έχουμε κρίσιμη απόσβεση.
Όταν ισχύει \(Λ < ω_ο \Rightarrow b^2 < 4 \cdot D \cdot m\) έχουμε ασθενή απόσβεση.
Από τις τρεις περιπτώσεις εμείς στο Λύκειο ασχολούμαστε μόνο με την ασθενή απόσβεση. Η εξίσωση κίνησης δηλαδή η λύση της διαφορικής εξίσωσης για την ασθενή απόσβεση είναι:
\[x = A \cdot e^{-Λt} \cdot ημ(ω_1t+φ)\]όπου η κυκλική συχνότητα της φθίνουσας ταλάνωσης δίνεται από την σχέση
\[ω_1^2 = ω_ο^2 - Λ^2 \Rightarrow ω_1 = \sqrt{\frac{D}{m} - (\frac{b}{2m})^2 }\]Άστοχες προτάσεις που αφορούν την φθίνουσα ταλάντωση:
Η θέση \(x=0\) είναι θέση ισορροπίας.
Στη θέση \(x=0\) το κινητό δεν έχει ταχύτητα.
Στη θέση \(x=0\) το κινητό έχει μέγιστη ταχύτητα.
Στη θέση ισορροπίας το κινητό πάντα απομακρύνεται από την θέση \(x=0\).
Σε κάθε περίοδο υπάρχει μια θέση ισορροπίας.
Καθώς περνά ο χρόνος οι ακραίες θέσεις στις οποίες φτάνει το κινητό παραμένουν ίδιες.
Οι θέσεις ισορροπίας του κινητού παραμένουν στο ίδιο σημείο.
Η σχέση \(Α = Α_ο \cdot e^{-Λt}\) μας δίνει το πλάτος της φθίνουσας ταλάντωσης.
Η ενέργεια και το πλάτος στην φθίνουσα ταλάντωση είναι εκθετικές συναρτήσεις του χρόνου.
Όταν η κινητική ενέργεια γίνεται μέγιστη, η δυναμική γίνεται ελάχιστη.
Για την καλύτερη κατανόηση των διαφορετικών περιπτώσεων (ισχυρή απόσβεση, κρίσιμη απόσβεση, ασθενής απόσβεση) και για χρήση μέσα στην σχολική αίθουσα δίνονται τα επόμενα κομμάτια κώδικα:
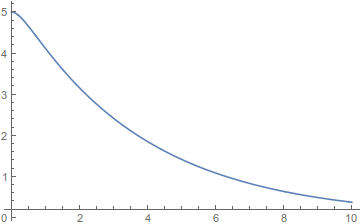
ισχυρή απόσβεση
DSolve[{x''[t] + 4 x'[t] + x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /. %, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ>ω_ο\) και το σχήμα
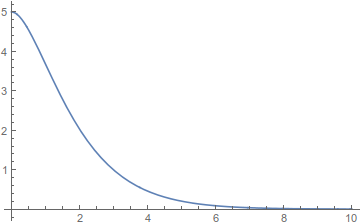
κρίσιμη απόσβεση
DSolve[{x''[t] + 2 x'[t] + x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /. %, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ=ω_ο\) και το σχήμα
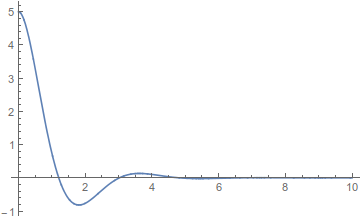
ασθενής απόσβεση (πρώτη περίπτωση)
DSolve[{x''[t] + 2 x'[t] + 4 x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /.%, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ<ω_ο\) και το σχήμα
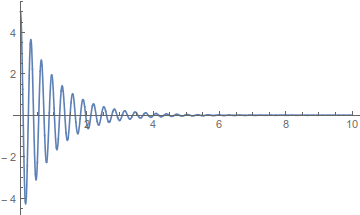
ασθενής απόσβεση (δεύτερη περίπτωση)
DSolve[{x''[t] + 2 x'[t] + 400 x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /. %, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ<ω_ο\) και το σχήμα
Ορισμοί για την Απλή Αρμονική Ταλάντωση
Ταλάντωση ονομάζεται μια περιοδική παλινδρομική κίνηση. Η ταλάντωση που γίνεται σε ευθεία τροχιά ονομάζεται γραμμική ταλάντωση. Απλή αρμονική ταλάντωση είναι μια ειδική περίπτωση γραμμικής ταλάντωσης σύμφωνα με την οποία ένα σώμα κινείται παλινδρομικά πάνω σε ένα άξονα γύρω από το σημείο Ο, που είναι μέσο της τροχιάς.
Περιοδικά φαινόμενα ονομάζονται τα φαινόμενα που εξελίσσονται και επαναλαμβάνονται αναλλοίωτα σε σταθερά χρονικά διαστήματα. Περίοδος ονομάζεται ο χρόνος που απαιτείται για να ολοκληρωθεί ένα περιοδικό φαινόμενο. Συχνότητα του περιοδικού φαινομένου ονομάζεται το πηλίκο του αριθμού των επαναλήψεων του φαινομένου προς τον αντίστοιχο χρόνο. Πλάτος της ταλάντωσης ονομάζεται η μέγιστη απομάκρυνση, δηλαδή η μέγιστη απόσταση από το σημείο Ο στην οποία φτάνει το κινητό.
Ορισμοί για την Φθίνουσα Ταλάντωση
Φθίνουσα ταλάντωση είναι μια ειδική περίπτωση γραμμικής ταλάντωσης σύμφωνα με την οποία ένα σώμα κινείται παλινδρομικά πάνω σε ένα άξονα γύρω από το σημείο Ο, που ονομάζεται σημείο αναφοράς. Στην φθίνουσα ταλάντωση η ενέργεια του κινητού συνεχώς μειώνεται.
Περίοδος ονομάζεται το χρονικό διάστημα μεταξύ δύο διαδοχικών διελεύσεων ενός κινητού από το σημείο Ο που ονομάζεται σημείο αναφοράς, με ταχύτητα ίδιας κατεύθυνσης. Συχνότητα ονομάζεται το πηλίκο του αριθμού των διελεύσεων του κινητού από το σημείο Ο, που ονομάζεται σημείο αναφοράς, με ταχύτητα ίδιας κατεύθυνσης.
blog comments powered by Disqus