Επιφανειακά κύματα Πανελλαδικές 2011 τα πρώτα τέσσερα ερωτήματα
Στην επιφάνεια ενός υγρού που ηρεμεί, βρίσκονται δύο σύγχρονες σημειακές πηγές \(Π_1\) και \(Π_2\), που δημιουργούν στην επιφάνεια του υγρού εγκάρσια αρμονικά κύματα ίσου πλάτους. Οι πηγές αρχίζουν να ταλαντώνονται τη χρονική στιγμή \(t_0=0\) ξεκινώντας από τη θέση ισορροπίας τους και κινούμενες προς την ίδια κατεύθυνση, την οποία θεωρούμε θετική. Η χρονική εξίσωση της ταλάντωσης ενός σημείου \(Μ\), που βρίσκεται στη μεσοκάθετο του ευθύγραμμου τμήματος \(Π_1Π_2\), μετά τη συμβολή των κυμάτων δίνεται στο \(SI\) από τη σχέση:
\[y_M = 0.2 ημ2π(5t-10)\]Η ταχύτητα διάδοσης των κυμάτων στην επιφάνεια του υγρού είναι \(υ_δ = 3 \frac{m}{s}\). Έστω \(Ο\) το μέσο του ευθύγραμμου τμήματος \(Π_1Π_2\) και \(d=1m\) η απόσταση μεταξύ των πηγών. Να βρείτε:
1. Την απόσταση \(ΜΠ_1\).
2. Τη διαφορά φάσης των ταλαντώσεων των σημείων \(Ο\) και \(Μ\).
3. Πόσα σημεία του ευθύγραμμου τμήματος \(Π_1Π_2\) ταλαντώνονται με μέγιστο πλάτος.
4. Να σχεδιάσετε τη γραφική παράσταση της απομάκρυνσης του σημείου \(Μ\) σε συνάρτηση με τον χρόνο \(t\) για \(0 \le t \le 2.5s\).
5. Πόσα σημεία του ευθύγραμμου τμήματος \(Π_1Π_2\) παραμένουν ακίνητα.
6. Να σχεδιάσετε τους κροσσούς ενισχυτικής συμβολής.
7. Να σχεδιάσετε τους κροσσούς καταστροφικής ή αποσβεστικής συμβολής.
Απάντηση:
1. Από τη σχέση που δίνεται υπολογίζουμε τα παρακάτω στοιχεία: \(Τ = 0.2s, A = 0.1m, λ = 0.6m, MΠ_1 = 6m\)
2. Από την αρχή της επαλληλίας έχουμε:
\[y = 2A συν2π \frac{r_1-r_2}{2λ} ημ2π(\frac{t}{T} - \frac{r_1+r_2}{2λ})\]για το σημείο \(Ο\) ισχύει \(r_1 = r_2 = 0.5\) άρα
\[y_o = 0.2 ημ 2π(5t - \frac{5}{6})\]οπότε για τη διαφορά φάσης των σημείων \(Μ\) και \(Ο\) έχουμε
\[Δφ = φ_Ο - φ_Μ = 2π(5t - \frac{5}{6}) - 2π(5t-10) \Rightarrow Δφ = \frac{55π}{3} rad\]3. Για τα σημεία που ταλαντώνονται με μέγιστο πλάτος ισχύει
\[συν2π \frac{r_1-r_2}{2λ} \pm 1 \Rightarrow 2π \frac{r_1-r_2}{2λ} = Nπ \Rightarrow r_1 - r_2 = 0.6N\]και επειδή τα σημεία ανήκουν στο ευθύγραμμο τμήμα \(Π_1Π_2\) ισχύει
\[r_1 + r_2 = 1\]οπότε λύνοντας το σύστημα και με δεδομένο ότι \(0 \le r_1 \le 1m\) βρίσκουμε τα σημεία \(r_1 = 0.2m\), \(r'_1 = 0.5m\) και \(r''_1 = 0.8m\), άρα τρία σημεία ταλαντώνονται με μέγιστο πλάτος.
4. Τέλος η γραφική παράστασης της χρονικής συνάρτησης απομάκρυνσης του σημείου \(Μ\) φαίνεται στο παρακάτω σχήμα. H διαταραχή φτάνει στο σημείο \(Μ\) την χρονική στιγμή \(t=2s\).
\[y_M = 0.2 ημ2π(5t-10) = 0.2 ημ10π(t-2)\]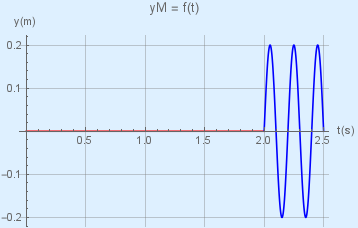
και ο κώδικας σε mathematica
f[t] := 0
g[t] := 0.2Sin[10Pi(t-2)]
Show[{Plot[f[t], {t, 0, 2}, PlotStyle -> Red],
Plot[g[t], {t, 2, 2.5}, PlotStyle -> Blue]},
PlotRange -> All,
GridLines -> Automatic,
Background -> LightBlue,
PlotLabel -> "yM = f(t)",
AxesLabel -> {"t(s)","y(m)"},
AxesOrigin -> {0, 0},
Filling -> Automatic]
5. Για τα σημεία που παραμένουν ακίνητα ισχύει
\[συν2π \frac{r_1-r_2}{2λ} =0 \Rightarrow 2π \frac{r_1-r_2}{2λ} = (2N+1) \frac{π}{2} \Rightarrow r_1 - r_2 = 0.6N+0.3\]και επειδή τα σημεία ανήκουν στο ευθύγραμμο τμήμα \(Π_1Π_2\) ισχύει
\[r_1 + r_2 = 1\]οπότε λύνοντας το σύστημα και με δεδομένο ότι \(0 \le r_1 \le 1m\) βρίσκουμε ότι τέσσερα σημεία παραμένουν συνεχώς ακίνητα, αφού
\[-\frac{6.5}{3} \le N \le \frac{3.5}{3}\]6. Έστω \(Σ\) σημείο με συντεταγμένες \((x, y)\) ως προς το καρτεσιανό σύστημα συντεταγμένων με αρχή το μέσον \(Ο\) του ευθύγραμμου τμήματος \(Π_1Π_2\), που ανήκει στον κροσσό ενυσχυτικής συμβολής. Για το σημείο \(Σ\) ισχύει:
\[r_1 - r_2 = Nλ\]Όλα τα σημεία που έχουν αυτή την ιδιότητα ανήκουν στην ίδια υπερβολή, άρα και τα σημεία τομής της υπερβολής με τον άξονα \(x'x, Α_1(-a, 0), Α_2(a, 0)\) όπως φαίνεται στο παρακάτω σχήμα:
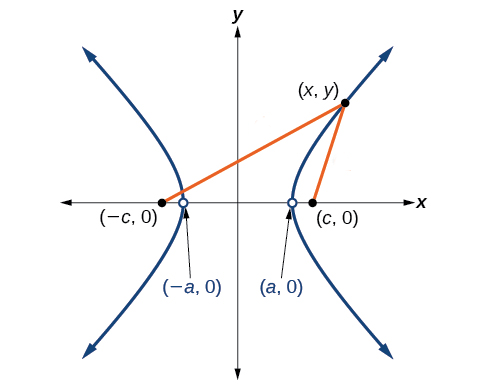
Οι πηγές έχουν συντεταγμένες \(Π_1(-c, 0), Π_2(c, 0)\) και όπως φαίνεται από την γεωμετρία του σχήματος ισχύει
\[r_1 - r_2 = 2a\]οπότε χρησιμοποιώντας το πυθαγόρειο θεώρημα και κάνοντας πράξεις έχουμε:
\[\sqrt{ (x+c)^2 + y^2} - \sqrt{ (x-c)^2 +y^2} = 2a \Rightarrow x^2(c^2 - a^2) - a^2 \cdot y^2 = a^2(c^2-a^2)\]και ανικαθιστώντας όπου \(c^2 - a^2 = b^2\) έχουμε τελικά την σχέση:
\[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\]η οποία είναι η εξίσωση της υπερβολής με κέντρο το σημείο \((0, 0)\) και εκκεντρότητα \(e = \frac{c}{a}\). Για την συγκεκριμένη άσκηση έχουμε \(Ν=-1, Ν=0, Ν=1\) δηλαδή τρεις υπερβολές εκ των οποίων η μία είναι η μεσοκάθετος στο ευθύγραμμο τμήμα \(Π_1Π_2\) για \(Ν=0\). Για να σχεδιάσουμε τις άλλες δύο υπερβολές (\(N = \pm 1\)) έχουμε
\[Νλ = 2a \Rightarrow a = \frac{Nλ}{2} \Rightarrow a= \pm 0.3, c=0.5, b=0.4\]οπότε η εξίσωση είναι:
\[\frac{x^2}{0.09} - \frac{y^2}{0.16} = 1\]η γραφική παράσταση φαίνεται στην επόμενη εικόνα
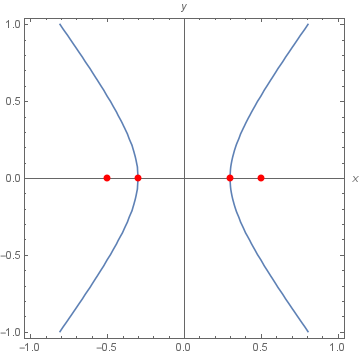
και ο κώδικας σε mathematica για τον σχεδιασμό της υπερβολής είναι:
ContourPlot[x^2/0.09 - y^2/0.16 == 1,
{x, -1, 1},
{y, -1, 1},
Axes->True,
AxesLabel -> {x, y},
Epilog -> {Red, PointSize[Large],
Point[ { {0.5, 0}, {0.3, 0}, {-0.3, 0}, {-0.5, 0} } ] } ]
7. Για τους κροσσούς καταστροφικής ή αποσβεστικής συμβολής ισχύουν
\[(2Ν+1) \frac{λ}{2} = 2a \Rightarrow a = (2N+1) \frac{λ}{4}\]και όπως δείξαμε στο \(5ο\) ερώτημα οι αποδεκτές τιμές για το \(Ν\) είναι \(Ν=0, Ν=1, Ν=-1, Ν=-2\). Άρα για το πρώτο ζευγάρι υπορβολών θα έχουμε για \(Ν=0\) ή \(Ν=-1\)
\(a=0.15\) ή \(a=-0.15 \Rightarrow a^2 = 0.0225, c=0.5 \Rightarrow c^2 = 0.25, b^2 = 0.2275\)
και η εξίσωση της υπερβολής είναι
\[\frac{x^2}{0.0225} - \frac{y^2}{0.2275} = 1\]ενώ για το δεύτερο ζευγάρι υπερβολών θα έχουμε για \(Ν=1\) ή \(Ν=-2\)
\(a=0.45\) ή \(a=-0.45 \Rightarrow a^2 = 0.2025, c=0.5 \Rightarrow c^2 = 0.25, b^2 = 0.0475\)
και η εξίσωση της υπερβολής είναι
\[\frac{x^2}{0.2025} - \frac{y^2}{0.0475} = 1\]η γραφική παράσταση φαίνεται στην επόμενη εικόνα
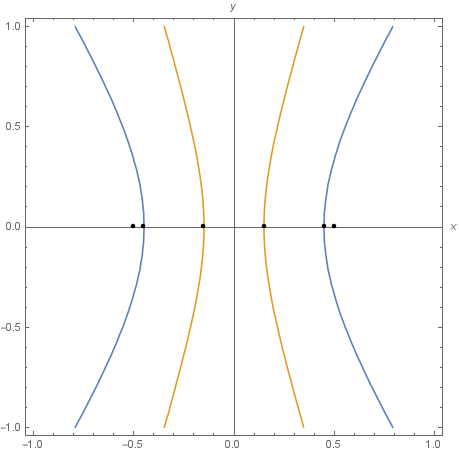
και ο κώδικας σε mathematica για τον σχεδιασμό των υπερβολών είναι:
ContourPlot[{x^2/0.2025 - y^2/0.475 == 1,
x^2/0.0225 - y^2/0.2275 == 1},
{x, -1, 1},
{y, -1, 1},
Axes->True,
AxesLabel -> {x, y},
Epilog -> {Black, PointSize[Medium],
Point[ { {0.5, 0},
{-0.45, 0},
{-0.15, 0},
{0.15, 0},
{0.45, 0},
{-0.5, 0} } ] } ]
blog comments powered by Disqus