Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2017
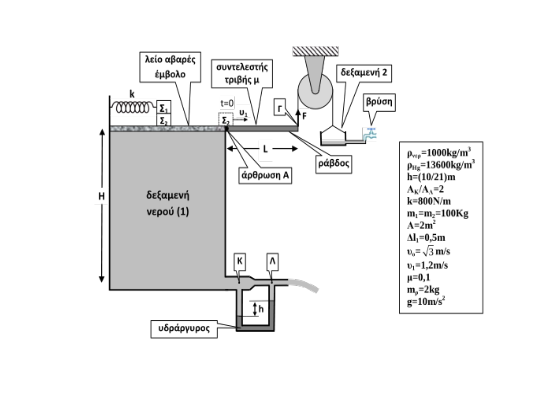
Δεξαμενή νερού (1) είναι στο πάνω τμήμα της κλειστή αεροστεγώς με οριζόντιο αβαρές έμβολο. Στην επιφάνεια του εμβόλου τοποθετούμε σώμα \(Σ_1\) μάζας \(m_1\) πάνω σε σώμα \(Σ_2\) μάζας \(m_2\). Μεταξύ \(Σ_1\) και \(Σ_2\) έχουμε τοποθετήσει κόλλα. Το σώμα \(Σ_1\) είναι στερεωμένο στο ένα άκρο οριζόντιου ελατηρίου με σταθερά \(k=800 \frac{Ν}{m}\). Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο σημείο όπως δίνεται στο σχήμα. Στη βάση της δεξαμενής υπάρχει ροόμετρο υδραργύρου από το οποίο εξέρχεται το νερό. H διαφορά στάθμης του υδραργύρου στο ροόμετρο είναι \(h= \frac{10}{21}m\), ενώ ο λόγος των διατομών (που θεωρούνται μικρές) στα σημεία Κ και Λ είναι \(\frac{Α_Κ}{Α_Λ}=2\). Αν δίνονται \(ρ_{νερ}=1000 \frac{kg}{m^3}\), \(ρ_{Hg}=13600 \frac{kg}{m^3}\), \(P_{atm}=10^5 Pa\), \(g=10\frac{m}{s^2}\),
1. Να υπολογιστεί η ταχύτητα \(υ_Λ\) του νερού στο σημείο \(Λ\).
2. Εάν τα σώματα \(Σ_1\), \(Σ_2\) έχουν μάζες \(m_1=m_2=100kg\) και η διατομή της δεξαμενής (1) είναι \(Α=2m^2\), να υπολογιστεί το ύψος \(H\) της δεξαμενής.
3. Συμπιέζουμε το ελατήριο ώστε να έχει συσπείρωση \(Δl_1=0,5m\) και κατόπιν εκτοξεύουμε το σύστημα \(Σ_1\) και \(Σ_2\) με αρχική ταχύτητα \(υ_ο= 3 \frac{m}{s}\), προς την θέση φυσικού μήκους του ελατηρίου. Αν το \(Σ_2\) χάνει την επαφή του με το \(Σ_1\) την στιγμή που η ταχύτητά του έχει μέτρο \(υ_1=1,2\frac{m}{s}\), να βρεθεί η μέγιστη οριζόντια δύναμη που αντέχει η κόλλα που συνδέει τα σώματα \(Σ_1\) και \(Σ_2\). Δίνεται ότι δεν υπάρχουν τριβές μεταξύ \(Σ_2\) και εμβόλου της δεξαμενής.
4. Το σώμα \(Σ_2\) ολισθαίνει χωρίς τριβές μέχρι την άρθρωση \(Α\) και στην συνέχεια ολισθαίνει πάνω στην οριζόντια ομογενή ράβδο \(Α\)Γ μήκους \(L\), όπου ο συντελεστής ολίσθησης είναι \(μ=0,1\). Η ράβδος μπορεί να περιστρέφεται χωρίς τριβές γύρω από την άρθρωση, αλλά στο σημείο \(Γ\) μέσω του νήματος και της τροχαλίας ασκείται στη ράβδο κατακόρυφη δύναμη \(F\) ώστε η ράβδος να ισορροπεί συνεχώς σε οριζόντια θέση. Αν το σώμα \(Σ_2\) σταματά να κινείται στο σημείο \(Γ\) ελάχιστα πριν έρθει σε επαφή με το νήμα, να βρεθεί το μήκος \(L\) της ράβδου.
5. Κατά τη διάρκεια της κίνησης του \(Σ_2\), η ράβδος είναι πάντα οριζόντια λόγω της δύναμης \(F\) από το νήμα. Στο άλλο άκρο του νήματος είναι δεμένη δεξαμενή 2 η οποία είναι αρχικά άδεια, αλλά μπορεί να τροφοδοτείται με νερό που εισέρχεται με οριζόντια ταχύτητα από βρύση. Η τροχαλία μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα όπως φαίνεται στο σχήμα. Αν η μάζα της ράβδου είναι \(m_ρ=2kg\), να γίνει η γραφική παράσταση της παροχής \(Π(t)\) της βρύσης σε συνάρτηση με τον χρόνο \(t\), ώστε η ράβδος να παραμένει συνεχώς οριζόντια. Θεωρήστε \(t=0\) την στιγμή που το \(Σ_2\) βρίσκεται στην άρθρωση \(Α\).
Απάντηση:
blog comments powered by Disqus