Ρευστά σε ισορροπία
Το δοχείο σχήματος U περιέχει υδράργυρο πυκνότητας \(ρ = 13.6 \frac{g}{cm^3}\) που ισορροπεί. Προσθέτουμε στο αριστερό σκέλος ένα υγρό \((1)\) πυκνότητας \(ρ_1 = 2 \frac{g}{cm^3}\) και στο δεξιό σκέλος άλλο υγρό \((2)\) με πυκνόητα \(ρ_2 = 0.8 \frac{g}{cm^3}\). Και τα δύο υγρά δεν αναμειγνύονται με τον υδράργυρο και ισορροπούν έτσι ώστε οι στάθμες τους να βρίσκονται στο ίδιο οριζόντιο επίπεδο. Το ύψος της στήλης του υγρού \((1)\) είναι \(h_1 = 25.6cm\). Κατά πόσο θα ανέβει η στάθμη του υδραργύρου και σε ποιο σκέλος του δοχείου;
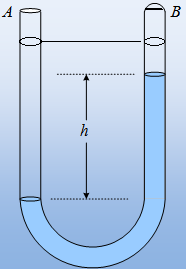
Όπως φαίνεται και από το σχήμα θα πρέπει να ισχύει
\[P_1 = P + P_2\]όπου \(Ρ_1\) η υδροστατική πίεση του υγρού στο αριστερό σκέλος, \(Ρ\) η πίεση του υδραργύρου στο δεξιό σκέλος σε βάθος \(h\) και \(Ρ_2\) η υδροστατική πίεση του υγρού στο δεξιό σκέλος. Κάνοντας χρήση του νόμου της υδροστατικής πίεσης έχουμε
\[ρ_1 \cdot g \cdot h_1 = ρ \cdot g \cdot h + ρ_2 \cdot g \cdot h_2 \Rightarrow 2000 \cdot 10 \cdot 0.256 = 13600 \cdot 10 \cdot h + 800 \cdot 10 \cdot h_2\]η οποία οδηγεί στην σχέση
\[136000 \cdot h + 8000 \cdot h_2 = 5120\]επίσης από το σχήμα έχουμε ότι
\[h_2 + h = h_1 \Rightarrow h_2 = 0.256 - h\]και αντικαθιστώντας στην προηγούμενη σχέση έχουμε
\[136000 \cdot h + 2048 - 8000 \cdot h = 5120 \Rightarrow 128000 \cdot h = 3072 \Rightarrow h = \frac{3072}{128000} \Rightarrow h = 0.024\]οπότε η απάντηση είναι \(0.024m\) στο δεξιό σκέλος.
blog comments powered by Disqus