Πανελλήνιος διαγωγισμός Φυσικής 2015
Δοχείο ημισφαιρικού σχήματος κέντρου \(Ο\) και ακτίνας \(R\) με τέλεια λεία τοιχώματα στερεώνεται σε οριζόντιο δάπεδο, κατά τρόπο ώστε η διάμετρος \(ΓΔ\) να είναι οριζόντια. Μέσα σε αυτό τοποθετείται πολύ λεπτή ομογενής ράβδος \(ΑΒ\) μήκους \(2 \cdot s\) (με \(s>R\)) και βάρους \(w\), η οποία αφήνεται να ισορροπήσει σχηματίζοντας γωνία \(θ\) με την οριζόντια διεύθυνση. Να υπολογίσετε:
Α. Tις δυνάμεις που δέχεται η ράβδος από το δοχείο,
Β. Tο μήκος \(ΑΓ=x\) του τμήματος της ράβδου που εξέχει από το δοχείο,
Γ. Tις τιμές της γωνίας \(θ\) για τις οποίες είναι δυνατή η ισορροπία της ράβδου.
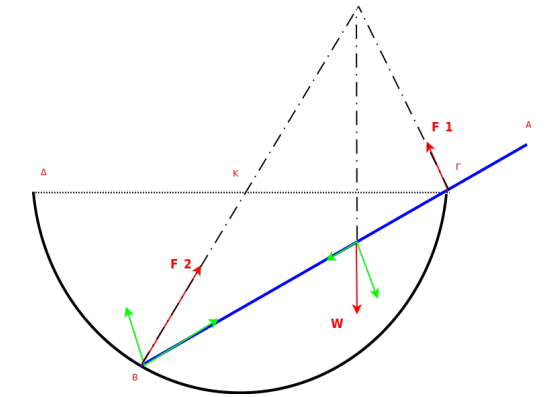
Α. Η δύναμη στο σημείο \(Β\) έχει ακτινική διεύθυνση, ενώ η δύναμη στο σημείο \(Γ\) είναι κάθετη στην ράβδο. Για να ισορροπεί η ράβδος θα πρέπει οι φορείς των δυνάμεων \(F_1, F_2\) και \(W\) να παιρνούν από το ίδιο σημείο, όπως φαίνεται στο σχήμα. Αφού αναλύσουμε την δύναμη \(F_2\) και την δύναμη \(W\) σε δύο συνιστώσες έχουμε για τον άξονα \(y\) που είναι κάθετος στην ράβδο:
\[ΣF_y = 0 \Rightarrow F_1 + F_2 \cdot ημθ = w \cdot συνθ\]ενώ για αυτόν κατά μήκος της ράβδου έχουμε:
\[ΣF_x = 0 \Rightarrow F_2 \cdot συνθ = W \cdot ημθ\]Λύνοντας το σύστημα των δύο εξισώσεων έχουμε για το πρώτο ερώτημα την απάντηση:
\[F_1 = \frac{w \cdot συν(2θ)}{συνθ}\]και
\[F_2 = \frac{w \cdot ημθ}{συνθ}\]Β. Το αλγεβρικό άθροισμα των ροπών ως προς το σημείο \(Β\) είναι μηδέν.
\[Στ = 0 \Rightarrow W \cdot s \cdot συνθ - F_1 \cdot (2s - x)\]και αντικαθιστώντας την τιμή για την \(F_1\) από το πρώτο ερώτημα έχουμε:
\[x = \frac{s \cdot (3 \cdot συν^2θ - 2)}{συν2θ}\]Γ. Το τρίγωνο \(ΚΒΓ\) είναι ισοσκελές. Φέρνουμε το ύψος που είναι και διάμεσος στην πλευρά \(ΒΓ\). Οπότε για το συνημίτονο της γωνίας έχουμε:
\[συνθ = \frac {2 \cdot s - x}{2 \cdot R}\]αντικαθιστώντας την τιμή του \(x\) από το προηγούμενο ερώτημα και γνωρίζοντας ότι το συνημίτονο της γωνίας αποκλείεται να είναι μηδέν έχουμε μετά τις πράξεις
\[συνθ = \frac {s + \sqrt(s^2 + 32 \cdot R^2)}{8 \cdot R}\]blog comments powered by Disqus