S.T.E.M.

Πανελλαδικές 2013

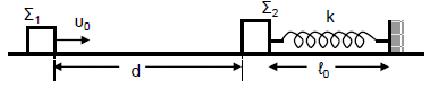
σχήμα

Σώμα \(Σ_1\) με μάζα \(m_1\) κινείται σε οριζόντιο επίπεδο ολισθαίνοντας προς άλλο σώμα \(Σ_2\) με μάζα \(m_2 = 2 * m_1\), το οποίο αρχικά είναι ακίνητο. Έστω \(υ_ο\) η ταχύτητα που έχει το σώμα \(Σ_1\) τη στιγμή \(t_ο = 0\) και ενώ βρίσκεται σε απόσταση \(d = 1 m\) από το σώμα \(Σ_2\). Αρχικά, θεωρούμε ότι το σώμα \(Σ_2\) είναι ακίνητο πάνω στο επίπεδο δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου με αμελητέα μάζα και σταθερά ελατηρίου \(k\), και το οποίο έχει το φυσικό του μήκος \(l_o\). Το δεύτερο άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο τοίχο, όπως φαίνεται στο σχήμα:

Αμέσως μετά τη κρούση, που είναι κεντρική και ελαστική, το σώμα \(Σ_1\) αποκτά ταχύτητα με μέτρο \(υ_1΄ = \sqrt 10 \frac ms\) και φορά αντίθετη της αρχικής ταχύτητας. Δίνεται ότι ο συντελεστής τριβής ολίσθησης των δύο σωμάτων με το οριζόντιο επίπεδο είναι \(μ = 0,5\) και ότι η επιτάχυνση της βαρύτητας είναι \(g = 10 \frac m{s^2}\).

  1. Να υπολογίσετε την αρχική ταχύτητα \(υ_o\) του σώματος \(Σ_1\).

  2. Να υπολογίσετε το ποσοστό της κινητικής ενέργειας που μεταφέρθηκε από το σώμα \(Σ_1\) στο σώμα \(Σ_2\) κατά την κρούση.

  3. Να υπολογίσετε το συνολικό χρόνο κίνησης του σώματος \(Σ_1\) από την αρχική χρονική στιγμή \(t_o\) μέχρι να ακινητοποιηθεί τελικά. Δίνεται: \(\sqrt 10 = 3,2\)

  4. Να υπολογίσετε τη μέγιστη συσπείρωση του ελατηρίου, αν δίνεται ότι \(m_2 = 1kg\) και \(k = 105 \frac Nm\).

Θεωρήστε ότι η χρονική διάρκεια της κρούσης είναι αμελητέα και ότι τα δύο σώματα συγκρούονται μόνο μία φορά.

Λύση της άσκησης με καθαρά υπολογιστικές μεθόδους και χρήση python.

Αρχικές συνθήκες

\[m = 1kg\] \[k = 105 \frac Nm\] \[u_o = 2 \cdot \sqrt10 \frac ms\] \[ball.m = 1\] \[ball.pos = vector(0,0,0)\] \[ball.vel = vector (2 \cdot \sqrt(10), 0, 0)\] \[t = 0\] 
        while ball.vel.x > 0:
                F_el = -105 * ball.pos
                T = vector(-5,0,0)
                F_net = F_el + T
                ball.vel = ball.vel + (F_net/ball.m}) * deltat
                ball.pos = ball.pos + ball.vel * deltat
                t = t + deltat
        print(t,ball.pos.x)

Η φυσική που χρησιμοποείτε για τον υπολογισμό της μέγιστης συσπείρωσης του ελατηρίου είναι:

Ο δεύτερος νόμος του νεύτωνα

\[ΣF = m \cdot α\] \[ball.vel = ball.vel + ( \frac {F_net}{ball.m}) \cdot deltat\]

όπου

\[ΣF = F_ελ + Τ = -k \cdot x – μ \cdot m \cdot g\]

και ο ορισμός του μεγέθους της ταχύτητας

\[u = \frac {Δx}{Δt}\] \[ball.pos = ball.pos + ball.vel \cdot deltat)\]

Την λύση της άσκησης μπορείτε να παρακολουθήσετε στο ακόλουθο link

blog comments powered by Disqus

Published

22 September 2013

Category

Άσκηση

Tags