Πανελλήνιες 2012 Θέμα Γ4
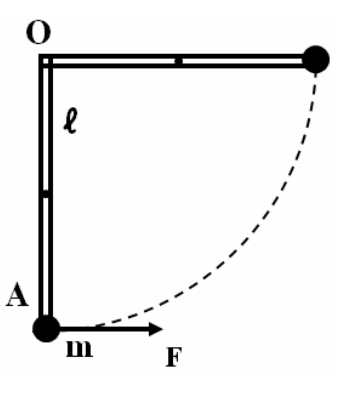
Ομογενής και ισοπαχής δοκός \((ΟΑ)\), μάζας \(M=6kg\) και μήκους \(l=0.3m\) μπορεί να στρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που περνά από το ένα άκρο της \(Ο\). Στο άλλο της άκρο \(Α\) υπάρχει στερεωμένη μικρή σφαίρα μάζας \(m = \frac{M}{2}\)
Ασκούμε στο άκρο Α δύναμη σταθερού μέτρου \(F = 30 \cdot \sqrt3 Ν\) που είναι συνεχώς κάθετη στη δοκό. Βρείτε τη γωνία που σχηματίζει η δοκός με την κατακόρυφο τη στιγμή που η κινητική της ενέργεια γίνεται μέγιστη. ∆ίνεται η ροπή αδράνειας ομογενούς δοκού μάζας \(Μ\) και μήκους \(l\) ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος σε αυτήν
\[Ι_{cm} = \frac{1}{12} \cdot M \cdot l^2\] \[ημ 60^0 = συν 30^0 = \frac{\sqrt3}{2}, ημ 30^0 = συν 60^0 = \frac{1}{2}\] \[g = 10 \frac{m}{s^2}\]Η λάθος λύση
Το σύστημα ράβδος-σώμα αποκτά μέγιστη κινητική ενέργεια όταν η γωνιακή ταχύτητα γίνεται μέγιστη. Αυτό συμβαίνει όταν η γωνιακή επιτάχυνση μηδενίζεται. Συνεπώς σε εκείνη την θέση στην οποία θα ισχύει
\[α_{γων} = 0 \Rightarrow Σ\vecτ =0\] \[F \cdot l = m \cdot g \cdot l \cdot συνθ + Μ \cdot g \cdot \frac{l}{2} \cdot συνθ \Rightarrow θ=60^0\]Βρίσκουμε πρώτα την ροπή αδράνειας του συστήματος ράβδος-σώμα ως προς τον άξονα περιστροφής \(Ο\).
\[I = I_ρ + Ι_m = \frac{1}{3} \cdot M \cdot l^2 + m \cdot l^2 = \frac{1}{3} \cdot M \cdot l^2 + \frac{1}{2} \cdot M \cdot l^2 = \frac{5}{6} \cdot M \cdot l^2 = 0.45kgm^2\]Για το σύστημα ράβδος-σώμα εφαρμόζουμε το Θ.Ε.Ε. από την κατώτερη θέση έως την θέση ανακύκλωσης
\[ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_F + W_B + W_β\] \[\frac{1}{2} \cdot I \cdot ω^2 = F \cdot s - M \cdot g \cdot l - m \cdot g \cdot 2 \cdot l\]και μετά τις πράξεις η γωνιακή ταχύτητα Βρίσκουμε ότι είναι περίπου \(ω = 7.5 \frac{r}{s}\) και αυτό σημαίνει ότι το σύστημα κάνει ανακύκλωση άρα σε κάθε κύκλο προστίθεται ενέργεια από την δύναμη \(F\) άρα δεν υπάρχει στιγμή που η κινητική ενέργεια είναι μέγιστη. Τελικά η ενέργεια απειρίζεται.
Μπορείτε να εκτυπώσετε τα θέματα από εδώ
blog comments powered by Disqus