Φυσική Serway Jewett
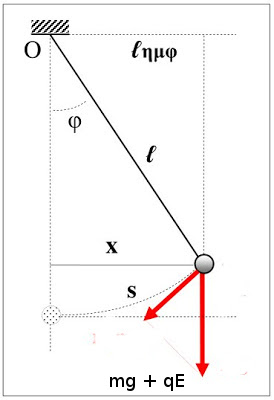
Μια μπάλα από φελλό μάζας \(1.00 g\) με φορτίο \(2.00 μC\) αναρτάται από ένα αβαρές νήμα μήκους \(0.500 m\) μέσα σε ένα ομογενές ηλεκτρικό πεδίο \(Ε = 1.00 \cdot 10^5 \frac{N}{C}\), το οποίο έχει κατεύθυνση κατακόρυφη προς τα κάτω. Αν η μπάλα μετατοπιστεί ελαφρά απο την κατακόρυφο, ταλαντώνεται σαν ένα απλό εκκρεμές.
α) Προσδιορίστε την περίοδο της ταλάντωσης.
β) Πρέπει να λάβετε υπόψη σας την επίδραση της βαρύτητας στους υπολογισμούς του ερωτήματος (α); Εξηγήστε.
Απάντηση:
Όπως φαίνεται στο σχήμα η κατακόρυφη δύναμη που δέχεται ο φελλός είναι \(m \cdot g + q \cdot E\). Αναλύουμε την δύναμη σε δυο συνιστώσες από τις οποίες μας ενδιαφέρει αυτή που έχει σχεδιαστεί. Αυτή είναι
\[ΣF = - (m \cdot g + q \cdot E) \cdot sinφ\]Η ροπή αυτής της δύναμης ως προς τον οριζόντιο άξονα που διέρχεται από το σημείο Ο είναι:
\[Στ = - (m \cdot g + q \cdot E) \cdot L \cdot sinφ\]όμως για την ροπή δύναμης γνωρίζουμε:
\[Στ = Ι \cdot a_{γων} \Rightarrow Στ = Ι \cdot \frac{dω}{dt} \Rightarrow Στ = Ι \cdot \frac{d^2φ}{dt^2}\]και αντικαθιστώντας την προηγούμενη σχέση φτάνουμε στην διαφορική εξίσωση:
\[- (m \cdot g + q \cdot E) \cdot L \cdot sinφ = Ι \cdot \frac{d^2φ}{dt^2}\]η ροπή αδράνεις είναι
\[Ι = m \cdot L^2\]οπότε μετά τις πράξεις έχουμε
\[- \frac{m \cdot g + q \cdot E}{m \cdot L} \cdot sinφ = \frac{d^2φ}{dt^2}\]κάνοντας την προσέγγιση
\[sinφ \approx φ\]έχουμε
\[- \frac{m \cdot g + q \cdot E}{m \cdot L} \cdot φ = \frac{d^2φ}{dt^2}\]από όπου βγάζουμε το συμπέρασμα ότι
\[ω^2 = \frac{m \cdot g + q \cdot E}{m \cdot L} \Rightarrow T = 2π \sqrt{\frac{m \cdot L}{m \cdot g + q \cdot E}}\]blog comments powered by Disqus