Κύλιση και με ολίσθηση και χωρίς

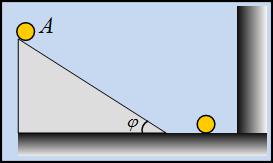
Όπως φαίνεται στο παραπάνω σχήμα, συμπαγής σφαίρα μάζας \(m\) και ακτίνας \(R\) εκτοξεύεται χωρίς περιστροφή προς μια κεκλιμένη εξέδρα η οποία σχηματίζει γωνία \(φ\) ως προς τον ορίζοντα. Την χρονική στιγμή \(t=0\) η σφαίρα έρχεται σε επαφή με την εξέδρα και έχει ταχύτητα \(u_ο\) κατά μήκος της εξέδρας. Στη συνέχεια παραμένει σε διαρκή επαφή με την εξέδρα (χωρίς να αναπηδά) εκτελώντας δύο διαφορετικές κινήσεις:

α) ολίσθηση και μερική περιστροφή μέχρι τον χρόνο \(t = t_1\) και β) κύλιση χωρίς ολίσθηση μετά τον χρόνο \(t = t_1\) μέχρι τον χρόνο \(t = t_2\) που η σφαίρα σταματάει προσωρινά.

Εάν ο συντελεστής τριβής ολίσθησης μεταξύ της σφαίρας και της εξέδρας είναι \(μ\), τότε να βρείτε:

1. Το μέτρο της τριβής ολίσθησης κατά την χρονική διάρκεια από \(t = 0\) έως \(t = t_1\).

2. Τη χρονική στιγμή που ξεκινάει η κύλιση χωρίς ολίσθηση.

3. Την ταχύτητα της σφαίρας την χρονική στιγμή εκκίνησης της κύλισης χωρίς ολίσθηση.

4. Το μέτρο της στατικής τριβής κατά την χρονική διάρκεια από \(t = t_1\) έως και \(t = t_2\).

Δίνεται η ροπή αδράνειας της σφαίρας \(Ι = \frac{2}{5} \cdot m \cdot R^2\) και η επιτάχυνση της βαρύτητας \(g\).

Απάντηση:

1. \[T = μ \cdot m \cdot g \cdot cos(φ)\]
2. \[t = \frac {2 \cdot u_o}{(2 \cdot g \cdot sin(φ)+7 \cdot g \cdot μ \cdot cos(φ))}\]
3. \[u = u_o - \frac {2 \cdot u_o \cdot (sin(φ)+μ \cdot cos(φ))}{(2 \cdot sin(φ)+7 \cdot μ \cdot cos(φ))}\]
4. \[T_s = \frac {2 \cdot m \cdot g \cdot sin(φ)}{7}\]