Ζεύγος Δυνάμεων
Ομογενής ράβδος μήκους \(L = 2m\) και μάζας \(m = 1kg\), είναι συνδεδεμένη στο ένα άκρο της με σημειακό αντικείμενο ίσης μάζας. Το σύστημα ράβδος - αντικείμενο τοποθετείται σε λείο οριζόντιο επίπεδο. Δίνεται η ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το κέντρο μάζας της
\[Ι = \frac{1}{12}\cdot m \cdot L^2\]Αν γνωρίζετε το μέτρο της οριζόντιας δύναμης \(F = 2N\), να υπολογίσετε την γωνιακή επιτάχυνση της ράβδου και την επιτάχυνση του κέντρου \(Κ\) της ράβδου σε κάθε μια από τις επόμενες περιπτώσεις:
(Όλα τα σχήματα αποτελούν κατόψεις)
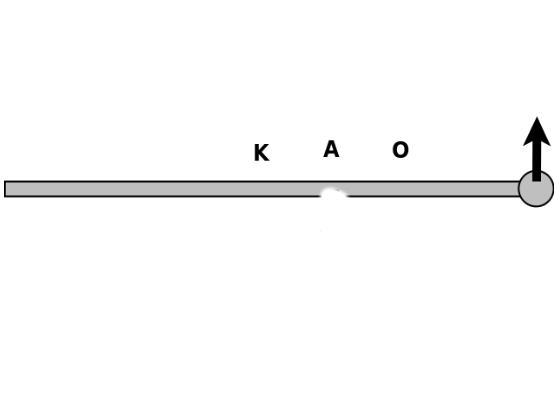
α) H δύναμη ασκείται στο σημειακό αντικείμενο που βρίσκεται στο άκρο της ράβδου.
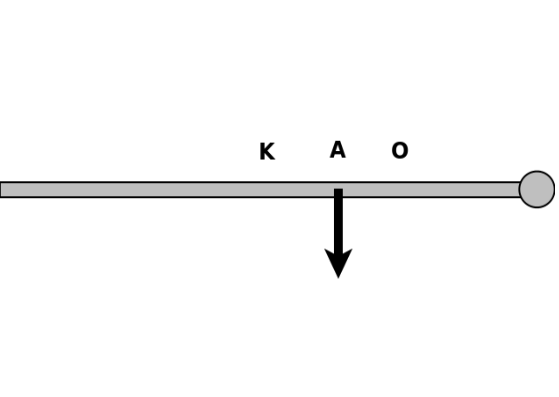
β) Η δύναμη ασκείται σε σημείο Α της ράβδου που απέχει από το κέντρο της ράβδου απόσταση \(ΚΑ = \frac{1}{4} m\).
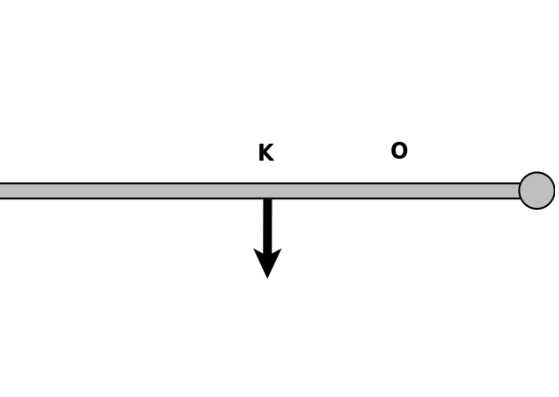
γ) H δύναμη ασκείται στο κέντρο \(Κ\) της ράβδου.
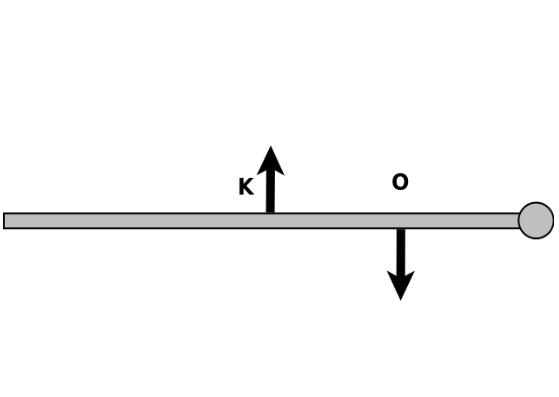
δ) Στη ράβδο ασκείται ζεύγος δυνάμεων μέτρου \(F = 2N\), από τις οποίες η μία ασκείται στο κέντρο \(Κ\) της ράβδου και η άλλη σε σημείο Ο που απέχει από το κέντρο \(Κ\) απόσταση \(ΚΟ = \frac{1}{2} m\).
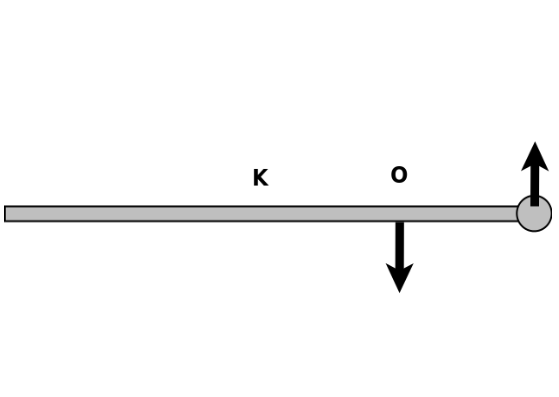
ε) Στη ράβδο ασκείται ζεύγος δυνάμεων μέτρου \(F = 2N\), από τις οποίες η μία ασκείται σε σημείο Ο που απέχει από το κέντρο \(Κ\) απόσταση \(ΚΟ = \frac{1}{2} m\) και η άλλη στο σημειακό αντικείμενο που βρίσκεται στο άκρο της ράβδου.
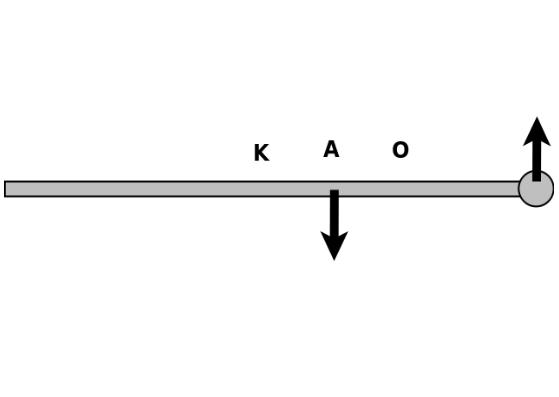
στ) Στη ράβδο ασκείται ζεύγος δυνάμεων μέτρου \(F = 2N\), από τις οποίες η μία ασκείται σε σημείο Α που απέχει από το κέντρο \(Κ\) απόσταση \(ΚΑ = \frac{1}{4} m\) και η άλλη στο σημειακό αντικείμενο που βρίσκεται στο άκρο της ράβδου.
Εάν η ράβδος περιστρέφεται γύρω από κατακόρυφο άξονα που διέρχεται από το ελεύθερο άκρο της, και στη ράβδο ασκείται το ζεύγος δυνάμεων της περίπτωσης στ) να βρείτε την δύναμη που ασκεί ο άξονας περιστροφής στην ράβδο.
Απάντηση:
α) Η γωνιακή επιτάχυνση της ράβδου έχει διεύθυνση κάθετη στο σχήμα και φορά προς την σελίδα. Η επιτάχυνση του κέντρου \(Κ\) έχει διεύθυνση κάθετη στην ράβδο και είναι ομμόροπη της δύναμης \(F\).
\[α_{γων} = \frac{6}{5} \frac{r}{s^2}, α_Κ = \frac{2}{5} \frac{m}{s^2}\]β) Η γωνιακή επιτάχυνση της ράβδου έχει διεύθυνση κάθετη στο σχήμα και φορά προς τον αναγνώστη. Η επιτάχυνση του κέντρου \(Κ\) έχει διεύθυνση κάθετη στην ράβδο και είναι ομμόροπη της δύναμης \(F\).
\[α_{γων} = \frac{3}{5} \frac{r}{s^2}, α_Κ = \frac{3}{20} \frac{m}{s^2}\]γ) Η γωνιακή επιτάχυνση της ράβδου έχει διεύθυνση κάθετη στο σχήμα και φορά προς τον αναγνώστη. Η επιτάχυνση του κέντρου \(Κ\) έχει διεύθυνση κάθετη στην ράβδο και είναι ομμόροπη της δύναμης \(F\).
\[α_{γων} = \frac{6}{5} \frac{r}{s^2}, α_Κ = \frac{8}{5} \frac{m}{s^2}\]δ) Η γωνιακή επιτάχυνση της ράβδου έχει διεύθυνση κάθετη στο σχήμα και φορά προς την σελίδα. Η επιτάχυνση του κέντρου \(Κ\) έχει διεύθυνση κάθετη στην ράβδο και φορά προς τα πάνω.
\[α_{γων} = \frac{6}{5} \frac{r}{s^2}, α_Κ = \frac{3}{5} \frac{m}{s^2}\]ε) Η γωνιακή επιτάχυνση της ράβδου έχει διεύθυνση κάθετη στο σχήμα και φορά προς τον αναγνώστη. Η επιτάχυνση του κέντρου \(Κ\) έχει διεύθυνση κάθετη στην ράβδο και φορά προς τα κάτω.
\[α_{γων} = \frac{6}{5} \frac{r}{s^2}, α_Κ = \frac{3}{5} \frac{m}{s^2}\]στ) Η γωνιακή επιτάχυνση της ράβδου έχει διεύθυνση κάθετη στο σχήμα και φορά προς τον αναγνώστη. Η επιτάχυνση του κέντρου \(Κ\) έχει διεύθυνση κάθετη στην ράβδο και φορά προς τα κάτω.
\[α_{γων} = \frac{9}{5} \frac{r}{s^2}, α_Κ = \frac{3}{5} \frac{m}{s^2}\] \[ΣF = \frac{27}{64} \cdot m N\]blog comments powered by Disqus