Οριζόντια γέφυρα
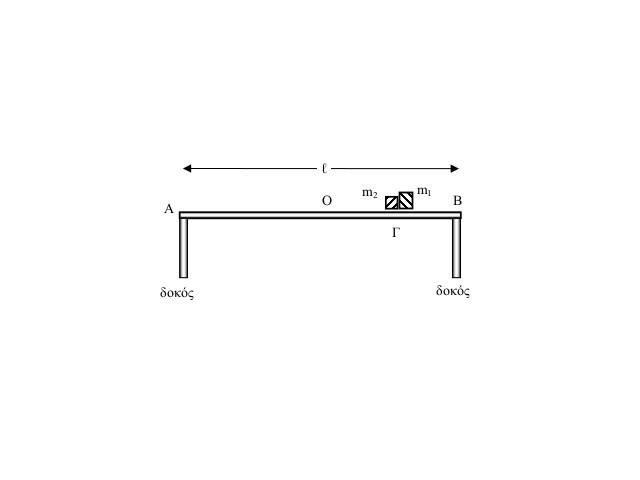
Πάνω σε ομογενή γέφυρα μήκους \(l = 100 m\) και μάζας \(M = 100 Kg\) βρίσκονται δύο κιβώτια μάζας \(m_1 = 80 Kg\) και \(m_2 = 20 Kg\). Η γέφυρα ισορροπεί οριζόντια στηριζόμενη σε δύο δοκούς στα άκρα της \(Α\) και \(Β\). Τα δύο κιβώτια αρχικά βρίσκονται ακίνητα στο ίδιο σημείο \(Γ\) το οποίο απέχει απόσταση \(ΓB = 25 m\) από το άκρο Β της γέφυρας (σχήμα).
Α1) Πόση είναι η κατακόρυφη δύναμη που δέχονται οι δοκοί \(Α\) και \(Β\) όταν τα δύο κιβώτια μένουν ακίνητα πάνω στη γέφυρα στο σημείο \(Γ\);
Β) Τη χρονική στιγμή \(t = 0\) το κιβώτιο \(m_1\) δέχεται τέτοια οριζόντια δύναμη ώστε αρχίζει να κινείται με σταθερή επιτάχυνση \(α_1 = 2 \frac{m}{s^2}\) προς τη μεριά του \(Β\), ενώ την ίδια στιγμή το κιβώτιο \(m_2\) εκσφενδονίζεται με αρχική ταχύτητα \(υ_0 = 20 \frac{m}{s}\) και κάνει ομαλά επιβραδυνόμενη κίνηση λόγω της Τριβής ολίσθησης που δέχεται. Αν το κιβώτιο \(m_2\) παρουσιάζει συντελεστή τριβής ολίσθησης με τη γέφυρα \(μ = 0.2\)
Β1) Να υπολογίσετε σε πόσο χρόνο φτάνουν τα κιβώτια στα άκρα της γέφυρας.
Β2) Να βρεθεί η συνάρτηση της κατακόρυφης δύναμης \(F_B\) που δέχεται ο δοκός \(Β\) με μεταβλητή τον χρόνο \(t\).
Β3) Να γίνει η γραφική παράσταση (σε βαθμολογημένους άξονες) της κατακόρυφης δύναμης \(F_B (t)\) σε σχέση με το χρόνο, από τη χρονική στιγμή \(t = 0\) μέχρι τη στιγμή που τα δύο κιβώτια φτάνουν στα άκρα της γέφυρας.
Β4) Πόση είναι μέγιστη τιμή της κατακόρυφης δύναμης \(F_{Amax}\) που δέχεται η δοκός Α;
∆ίνεται η επιτάχυνση της βαρύτηττας \(g = 10 \frac{m}{s^2}\)
Απάντηση:
blog comments powered by Disqus