Μέτρηση της ροπής αδράνειας
Μέτρηση της ροπής αδράνειας (Δυναμική προσέγγιση)
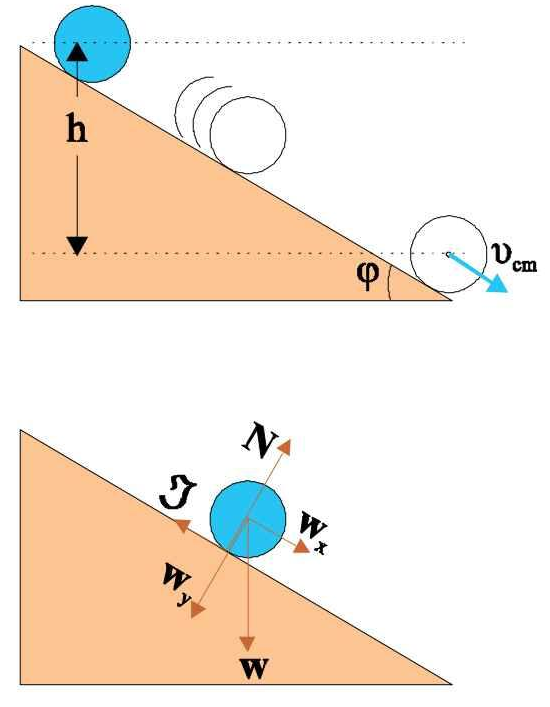
Κατά την κύλιση ενός στερεού πάνω σε πλάγιο επίπεδο, κάθε σημείο του στερεού έρχεται διαδοχικά σε επαφή με το επίπεδο. Έτσι όταν το στερεό σε χρόνο \(dt\) μετακινηθεί κατά \(ds\), ένα σημείο \(Α\) της περιφέρειας του στερεού θα έχει στραφεί κατά τόξο μήκους \(ds\) στο οποίο αντιστοιχεί η επίκεντρη γωνία \(dθ\). Η ταχύτητα του κέντρου μάζας του στερεού είναι:
\[υ_{cm} = \frac{ds}{dt} \Rightarrow υ_{cm} = \frac{R \cdot dθ}{dt} \Rightarrow υ_{cm} = ω \cdot R\]H γωνιακή ταχύτητα \(ω = \frac{dθ}{dt}\) του στερεού αυξάνεται, δηλαδή το στερεό έχει γωνιακή επιτάχυνση \(α_{γων} =\frac{dω}{dt}\). To κέντρο μάζας του στερεού εκτελεί ομαλά επιταχυνόμενη κίνηση και η επιτάχυνση του κέντρου μάζας δίνεται από την σχέση:
\[α_{cm} = \frac{dυ_{cm}}{dt} \Rightarrow α_{cm} = \frac{dω}{dt} \cdot R \Rightarrow α_{cm} = α_{γων} \cdot R\]Η κύλιση του στερεού οφείλεται στην τριβή. Η ροπή της τριβής ως προς τον άξονα συμμετρίας του στερεού είναι αυτή που περιστρέφει το στερεό. Η τριβή δεν μετατοπίζει το σημείο της εφαρμογής της, αφού κάθε στιγμή ασκείται σε διαφορετικό σημείο του στερεού. Πρόκειται δηλαδή για στατική τριβή. Μια ομάδα μαθητών μελετούν το φαινόμενο “ΚΥΛΙΣΗ ΣΤΕΡΕΟΥ ΣΕ ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ”. Διαθέτουν κεκλιμένο επίπεδο, φωτοπύλες και μετροταινία. Για τη μέτρηση του χρόνου με τη μέγιστη ακρίβεια χρησιμοποιούν ψηφιακούς χρονομετρητές που διεγείρονται από ειδικά αισθητήρια υπέρυθρης ακτινοβολίας, τις φωτοπύλες. Επειδή οι δυνάμεις που ασκούνται στο στερεό κατά την κίνησή του στο κεκλιμένο επίπεδο είναι σταθερές, η κίνηση του κέντρου μάζας του είναι ομαλά επιταχυνόμενη. Για την κίνηση του κέντρου μάζας ισχύει η σχέση:
\[l = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow α_{cm} = \frac{2l}{t^2}\]Έτσι οι μαθητές μετρώντας με την μετροταινία το μήκος του κεκλιμένου επιπέδου και με τις φωτοπύλες την χρονική διάρκεια της κίνησης του στερεού υπολογίζουν την επιτάχυνση του κέντρου μάζας του στερεού. Για κάθε κλίση, μετρούν κάθε φορά το ύψος \(h\) του σημείου απ’ όπου ξεκινάει η κίνηση του στερεού. Οι μαθητές φροντίζουν η γωνία του κεκλιμένου επιπέδου να είναι μικρή, ώστε να λάβει χώρα κύλιση χωρίς ολίσθηση. Επαναλαμβάνουν το πείραμα και καταγράφουν τα αποτελέσματά τους στον πίνακα που ακολουθεί:
\[\begin{array}{c c} t (s) & h(m) \\ 1.000 & 0.10 \\ 0.816 & 0.15 \\ 0.707 & 0.20 \\ 0.632 & 0.25 \\ 0.577 & 0.30 \\ 0.534 & 0.35 \\ 0.500 & 0.40 \\ \end{array}\]Θεωρήστε δεδομένη την επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\), την ροπή αδράνειας ενός στερεού \(Ι = m \cdot D^2\) και το μήκος του κεκλιμένου επιπέδου \(l = 0.5m\).
Να σχεδιάσετε την γραφική παράσταση της επιτάχυνσης του κέντρου μάζας του στερεού συναρτήση του ύψους και με την βοήθεια του 2ου Νόμου του Νεύτωνα και για την μεταφορική και για την στροφική κίνηση και της κλίσης της γραφικής παράστασης, να βρείτε αν το στερεό που κυλίεται στο κεκλιμένο επίπεδο είναι:
α. Μια συμπαγής σφαίρα ακτίνας \(R\) με ροπή αδράνειας \(Ι = \frac{2}{5} \cdot m \cdot R^2\)
β. Ένας συμπαγής κύλινδρος ακτίνας \(R\) με ροπή αδράνειας \(Ι = \frac{1}{2} \cdot m \cdot R^2\)
γ. Ένας κοίλος κύλινδρος ακτίνας \(R\) με ροπή αδράνειας \(Ι = m \cdot R^2\)
α) Να επιλέξετε την σωστή απάντηση.
β) Να δικαιολογήσετε την επιλογή σας.
Για τον υπολογισμό του συντελεστή διεύθυνσης της ευθείας να γίνει χρήση της σχέσης \(λ = \frac{y_2 - y_1}{x_2 - x_1}\) με τις συντεταγμένες μόνο της αρχικής και της τελικής μέτρησης.
blog comments powered by Disqus