Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2019
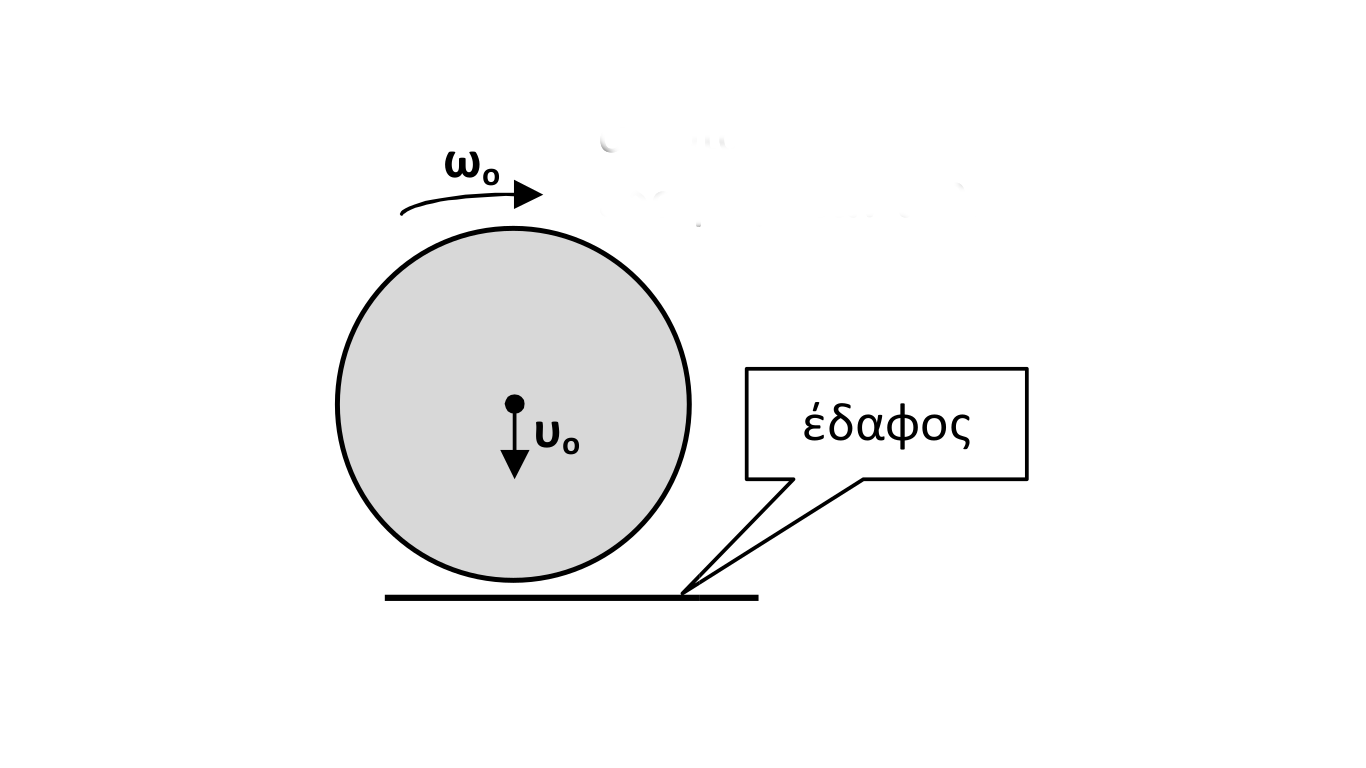
Ομογενής κύλινδρος ακτίνας \(R\) και μάζας \(m\), με ροπή αδράνειας \(I= \frac{1}{2} \cdot m \cdot R^2\) γύρω από άξονα που περνά από τα κέντρα των βάσεών του, αφήνεται περιστρεφόμενος να πέσει στο έδαφος από μικρό ύψος. Τη στιγμή \(t=0\) ο κύλινδρος φτάνει στο έδαφος έχοντας μεταφορική ταχύτητα \(υ_ο\) προς τα κάτω και γωνιακή ταχύτητα \(ω_ο\) γύρω από τον άξονα που αναφέρθηκε παραπάνω με τον άξονα αυτό να είναι οριζόντιος όπως φαίνεται στο παραπάνω σχήμα. Η κατακόρυφη συνιστώσα της μεταφορικής ταχύτητας του κυλίνδρου μηδενίζεται όταν \(t=t_1\) και για \(t>t_1\) συνεχίζει να είναι ίση με 0, δηλαδή ο κύλινδρος δεν αναπηδά. Στο επόμενο σχήμα δίνεται η γραφική παράστασηη της κάθετης δύναμης \(N\) που ασκεί το έδαφος στον κύλινδρο ως συνάρτηση του χρόνου.
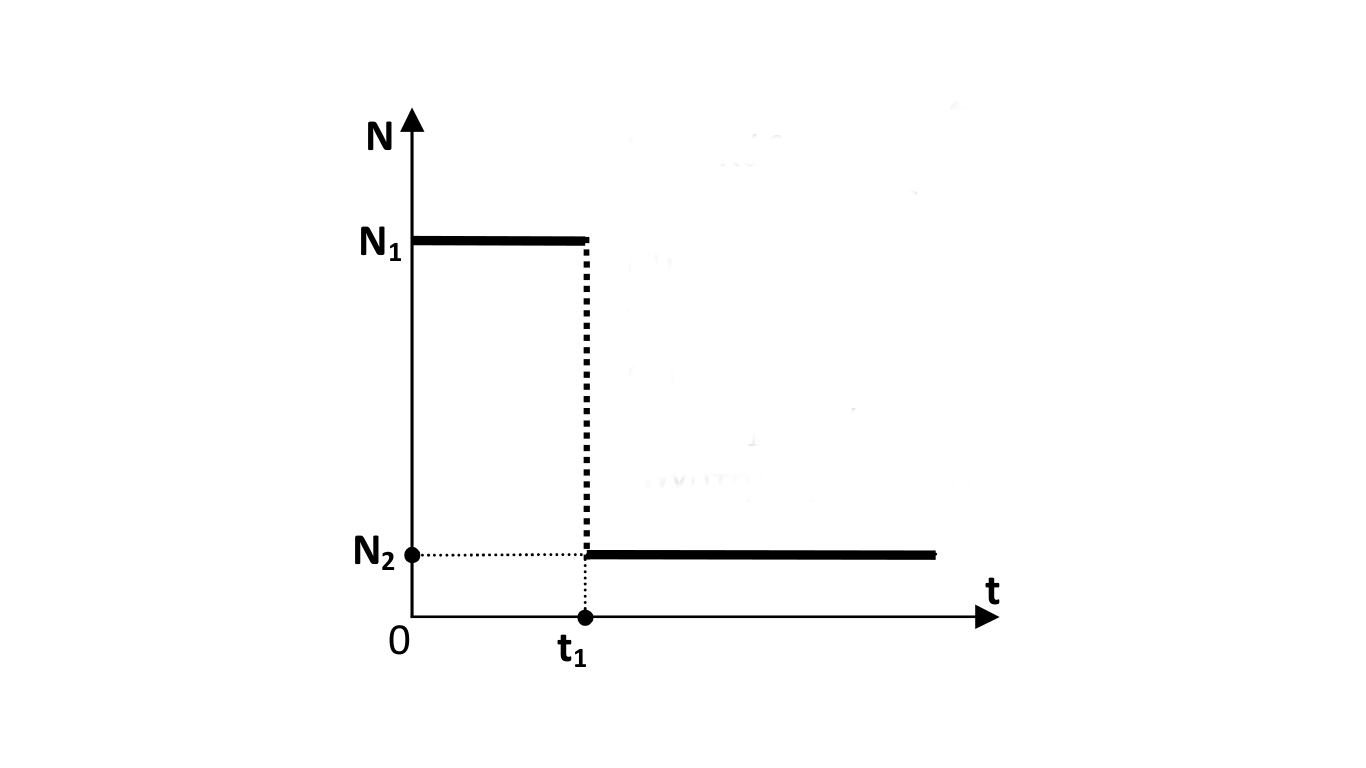
Κατά την διάρκεια της επαφής του κυλίνδρου με το έδαφος, ο κύλινδρος αρχικά σπινιάρει. Ο κύλινδρος παραμορφώνεται ελάχιστα έτσι ώστε να θεωρούμε ότι δεν μεταβάλλεται η ροπή αδράνειας του. Ο συντελεστής τριβής μεταξύ κυλίνδρου και εδάφους είναι \(μ≠0\). Ο κύλινδρος σπινιάρει στο έδαφος μέχρι το χρόνο \(t_2\) , ενώ η επιτάχυνση της βαρύτητας είναι ίση με \(g\).
1. Να δείξετε ότι όταν θα σταματήσει το σπινιάρισμα του κυλίνδρου στο έδαφος, τότε \(υ_{cm} =ω \cdot R\), όπου \(υ_{cm}\) η οριζόντια μεταφορική ταχύτητα.
2. Αν \(t_2 ≤ t_1\) και κατά τη διάρκεια του σπινιαρίσματος, να βρείτε την μεταφορική επιτάχυνση \(α_{cm}\) στον οριζόντιο άξονα \(x\) και την γωνιακή επιβράδυνση \(α_{γων}\) του κυλίνδρου, σε σχέση με τα δεδομένα της άσκησης.
3. Να δείξετε ότι αν \(t_2 ≤ t_1\), η γωνιακή ταχύτητα \(ω_1\) του κυλίνδρου μετά το σπινιάρισμα, εξαρτάται μόνο από την \(ω_ο\) και να βρείτε την τιμή της.
4. Να δείξετε ότι αν \(t_2 > t_1\) , η γωνιακή ταχύτητα \(ω_2\) του κυλίνδρου μετά το πέρας της ολίσθησης, εξαρτάται μόνο από την \(ω_ο\) και να βρείτε την τιμή της.
Θεωρούμε γνωστά την ροπή αδράνειας του κυλίνδρου \(Ι = \frac{1}{2} \cdot m \cdot R^2\), την επιτάχυνση της βαρύτητας \(g\), την ακτίνα της βάσης \(R\), την αρχική ταχύτητα \(υ_ο\), τον συντελεστή τριβής ολίσθησης \(μ\) και τον χρόνο \(t_1\).
1. Όταν σταματήσει το σπινιάρισμα ξεκινάει η κύλιση του κυλίνδρου. Κατά την κύλιση κάθε σημείο της επιφάνειας του κυλίνδρου έρχεται διαδοχικά σε επαφή με το έδαφος. Έτσι όταν ο κύλινδρος σε χρόνο \(dt\) μετακινηθεί κατά \(ds\), ένα σημείο \(Α\) της περιφέρειας του θα έχει στραφεί κατά τόξο μήκους \(ds\), στο οποίο αντιστοιχεί η επίκεντρη γωνία \(dθ\). Η ταχύτητα του κέντρου μάζας του κυλίνδρου είναι \(υ_{cm} = \frac{ds}{dt}\) όμως \(dθ = \frac{ds}{R} \Rightarrow ds = R \cdot dθ\) και αντικαθιστώντας έχουμε \(υ_{cm} = R \cdot \frac{dθ}{dt}\) και επειδή \(\frac{dθ}{dt} = ω\) έχουμε τελικά \(υ_{cm} =ω \cdot R\).
2. Την χρονική στιγμή \(t=t_1\) μηδενίζεται η κατακόρυφη ταχύτητα του κυλίνδρου, ενώ την χρονική στιγμή \(t=t_2\) ξεκινάει η κύλιση (χωρίς ολίσθηση) του κυλίνδρου.
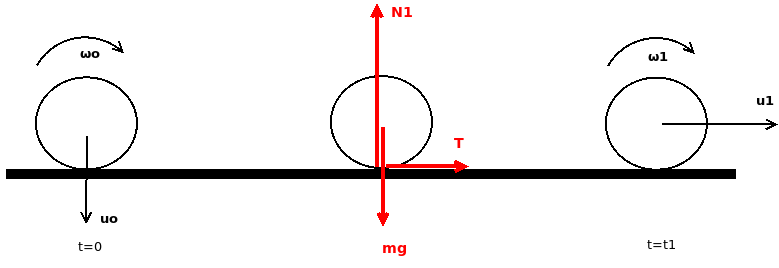
Στο παραπάνω σχήμα έχουν σχεδιαστεί τρία στιγμιότυπα από την κίνηση του κυλίνδρου. Στο πρώτο και στο τελευταίο σχεδιάστηκαν οι ταχύτητες, κέντρου μάζας και γωνιακές του κυλίνδρου ενώ στο μεσαίο σχεδιάστηκαν οι δυνάμεις που ασκούνται στον κύλινδρο. Η μεταφορική κίνηση στον άξονα \(x\) είναι επιταχυνόμενη, στον άξονα \(y\) είναι επιβραδυνόμενη, ενώ η στροφική γύρω από το κέντρο μάζας του κυλίνδρου είναι επιβραδυνόμενη λόγω της ροπής της τριβής ολίσθησης.
\[ΣF_y = m \cdot α_y \Rightarrow N_1 - m \cdot g= m \frac{Δυ_y}{Δt} \Rightarrow N_1 = m \cdot g + m \frac{υ_ο}{t_1}\] \[T = μ \cdot N_1 \Rightarrow T = μ \cdot m \cdot (g + \frac{υ_ο}{t_1})\] \[Στ = Ι \cdot α_{γων} \Rightarrow α_{γων} = \frac{T \cdot R}{I} \Rightarrow α_{γων} = \frac{2μ}{R}\cdot (g + \frac{υ_ο}{t_1})\] \[ΣF_x = m \cdot α_{cm} \Rightarrow T = m \cdot α_{cm} \Rightarrow α_{cm} = μ \cdot (g + \frac{υ_ο}{t_1})\]3. επιβραδυνόμενη περιστροφική κίνηση
\[ω_1 = ω_ο - α_{γων} \cdot t_2 \Rightarrow ω_1 = ω_ο - \frac{2μ}{R} \cdot (g + \frac{υ_ο}{t_1})\cdot t_2\]επιταχυνόμενη μεταφορική κίνηση
\[υ_1 = α_{cm} \cdot t_2 \Rightarrow υ_1 = μ\cdot (g + \frac{υ_ο}{t_1})\cdot t_2\]και αφού την χρονική στιγμή \(t = t_2\) ξεκινάει η κύλιση (χωρίς ολίσθηση) θα ισχύει
\[υ_1 = ω_1 \cdot R \Rightarrow μ\cdot (g + \frac{υ_ο}{t_1})\cdot t_2 = (ω_ο - \frac{2μ}{R} \cdot (g + \frac{υ_ο}{t_1})\cdot t_2)\cdot R\]και μετά τις πράξεις υπολογίζουμε την χρονική στιγμή \(t=t_2\)
\[t_2 = \frac{ω_ο\cdot R}{3\cdot μ \cdot (g + \frac{υ_ο}{t_1})}\]οπότε με γνωστό τον χρόνο υπολογίζουμε την ζητούμενη γωνιακή ταχύτητα
\[ω_1 = ω_ο - \frac{2μ}{R} \cdot (g + \frac{υ_ο}{t_1})\cdot t_2 \Rightarrow ω_1 = ω_ο - \frac{2μ}{R} \cdot (g + \frac{υ_ο}{t_1})\cdot \frac{ω_ο\cdot R}{3\cdot μ \cdot (g + \frac{υ_ο}{t_1})} \Rightarrow ω_1 = \frac{ω_ο}{3}\]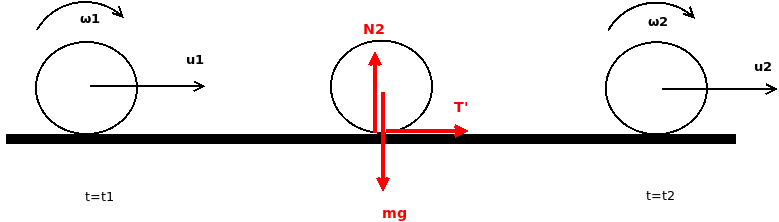
4. Όταν ισχύει \(t_2 > t_1\) δηλαδή ξεκινάει η κύλιση μετά τον μηδενισμό της κατακόρυφης συνιστώσας της ταχύτητας αλλάζει η κάθετη δύναμη από το έδαφος και άρα και η τριβή.
\[ΣF_y = m \cdot α_y \Rightarrow N_2 - m \cdot g= 0 \Rightarrow N_2 = m \cdot g\] \[T' = μ \cdot N_2 \Rightarrow T' = μ \cdot m \cdot g\] \[Στ = Ι \cdot α'_{γων} \Rightarrow α'_{γων} = \frac{T' \cdot R}{I} \Rightarrow α'_{γων} = \frac{2μ}{R}\cdot g\] \[ΣF_x = m \cdot α'_{cm} \Rightarrow T = m \cdot α'_{cm} \Rightarrow α'_{cm} = μ \cdot g\]Δηλαδή αλλάζει και η γωνιακή επιτάχυνση και η επιτάχυνση του κέντρου μάζας.
Την χρονική στιγμή \(t=t_1\) ισχύουν από την προηγούμενη κίνηση τα παρακάτω:
\[ω_1 = ω_ο - α_{γων} \cdot t_1 \Rightarrow ω_1 = ω_ο - \frac{2μ}{R} \cdot (g + \frac{υ_ο}{t_1})\cdot t_1 \Rightarrow ω_1 = ω_ο - \frac{2μ}{R} \cdot (υ_ο + g\cdot t_1)\] \[υ_1 = α_{cm} \cdot t_1 \Rightarrow υ_1 = μ\cdot (g + \frac{υ_ο}{t_1})\cdot t_1 \Rightarrow υ_1 = μ\cdot (υ_ο + g\cdot t_1)\]ενώ για την χρονική στιγμή \(t=t_2\) έχουμε
\[υ_2 = υ_1 + α'_{cm} \cdot (t_2 - t_1)\] \[ω_2 = ω_1 - α'_{γων} \cdot (t_2 - t_1)\] \[υ_2 = ω_2 \cdot R\]κάνοντας αντικατάσταση στην τελευταία σχέση βρίσκουμε μετά τις πράξεις την χρονική διάρκεια \((t_2 - t_1)\)
\[t_2 - t_1 = \frac{ω_1 \cdot R - υ_1}{α'_{cm} + α'_{γων} \cdot R}\]και αντικαθιστώντας στην γωνιακή ταχύτητα
\[ω_2 = ω_1 - α'_{γων} \cdot \frac{ω_1 \cdot R - υ_1}{α'_{cm} + α'_{γων} \cdot R} \Rightarrow ω_2 = \frac{ω_ο}{3}\]blog comments powered by Disqus