Ρευστά Διαγωνισμός Φυσικής 2017
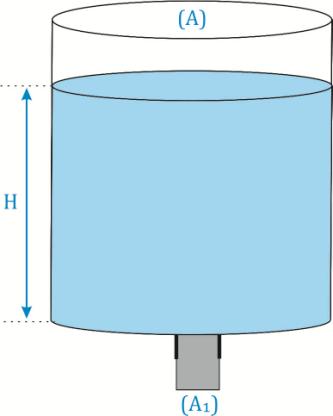
Ανοικτό κυλινδρικό δοχείο εμβαδού διατομής \(Α\) περιέχει νερό μέχρι ύψους \(Η\). Στον πυθμένα φέρει οπή εμβαδού \(A_1 = \frac{A}{3}\) κλεισμένη με πώμα. Η επιτάχυνση της βαρύτητας είναι \(g\). Τη χρονική στιγμή \(t=0\) τραβάμε ακαριαία το πώμα από την οπή και το νερό αρχίζει να ρέει ανεμπόδιστα. Να αποδείξετε ότι ο ολικός χρόνος που απαιτείται ώστε να αδειάσει το δοχείο δίνεται από τη σχέση \(t_{ολ} = 4 \cdot \sqrt{\frac{H}{g}}\).
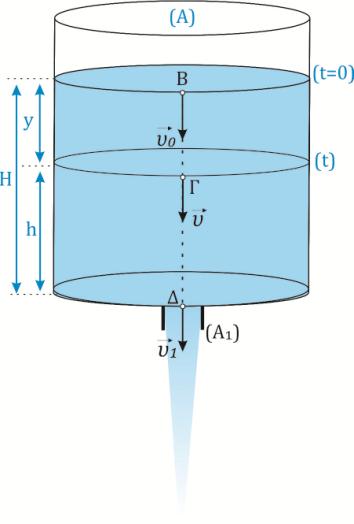
Τη χρονική στιγμή \(t = 0\) τραβάμε ακαριαία το πώμα από την οπή. Έστω \(υ_ο\) το μέτρο της ταχύτητας ροής των σημείων της επιφάνειας του νερού αρχικά. Μια τυχαία χρονική στιγμή \(t\) που η στάθμη έχει κατέβει κατά \(y\) το μέτρο της ταχύτητας ροής των σημείων της επιφάνειας του νερού είναι \(υ\), ενώ η ταχύτητα εκροής από την οπή είναι \(υ_1\). Εφαρμόζουμε την εξίσωση Bernoulli κατά μήκος μιας ρευματικής γραμμής από το σημείο Γ στο σημείο Δ.
\[p_Γ + \frac{1}{2} \cdot ρ \cdot υ^2 + ρ \cdot g \cdot h= p_Δ + \frac{1}{2} \cdot ρ \cdot υ_1^2\]Αλλά \(p_Γ = p_Δ = p_{ατμ}\), οπότε η σχέση γίνεται
\[υ_1^2 = υ^2 +2 \cdot g \cdot h\]Εάν εφαρμόσουμε και την εξίσωση συνέχειας έχουμε \(Α \cdot υ = A_1 \cdot υ_1\). Όμως ισχύει \(h = H -y\), άρα έχουμε τελικά
\[υ^2 = \frac{g \cdot H}{4} - \frac{g}{4}\cdot y\]Η παραπάνω σχέση χαρακτηρίζει κάθε ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση οπότε:
\[υ_ο = \sqrt{\frac{g\cdot H}{4}}\]και \(α = \frac{g}{8}\).
Οπότε τελικά έχουμε
\[υ = υ_ο - α \cdot t \Rightarrow υ = \sqrt{\frac{g\cdot H}{4}} - \frac{g}{8} \cdot t \Rightarrow t = 4\cdot \sqrt{\frac{H}{g}}\]blog comments powered by Disqus