Φθίνουσα ταλάντωση και Mathematica
Μελέτη της φθίνουσας ή αποσβεννύμενης ταλάντωσης με την βοήθεια του λογισμικού “Mathematica”
Στην φθίνουσα ταλάντωση εκτός από την δύναμη επαναφοράς
\[F = -D \cdot x\]που εφαρμόζεται στο υλικό σημείο ασκείται και η δύναμη απόσβεσης
\[F' = - b \cdot υ\]Τέτοια δύναμη είναι η δύναμη αντίστασης που ασκείται σε μικρά αντικείμενα που κινούνται μέσα στον αέρα ή μέσα σε υγρό. Το b ονομάζεται σταθερά απόσβεσης και εξαρτάται από:
α) τις ιδιότητες του μέσου
β) το σχήμα του αντικειμένου
γ) το μέγεθος του αντικειμένου.
Κάνοντας χρήση του 2ου νόμου του Νεύτωνα έχουμε:
\[ΣF = m \cdot α \Rightarrow F + F' = m \cdot a\]και κάνοντας αντικατάσταση έχουμε:
\[-D \cdot x - b \cdot υ = m \cdot \frac{d^2x}{dt^2} \Rightarrow m \cdot \frac{d^2x}{dt^2} + D \cdot x + b \cdot υ =0\]H παρακάτω διαφορική εξίσωση είναι μια γραμμική ομογενής 2ας τάξης και παρατίθεται ο κώδικας που την λύνει για διαφορετικές τιμές των παραμέτρων.
\[\frac{d^2x}{dt^2} + \frac{b}{m} \cdot \frac{dx}{dt} + \frac{D}{m} \cdot x = 0\]H σταθερά που εξαρτάται από την σταθερά απόσβεσης και τη μάζα του ταλαντούμενου σώματος συμβολίζεται με Λ και ονομάζεται εκθέτης απόσβεσης \(Λ = \frac{b}{2m}\). Εάν αντικαταστήσουμε τον λόγο \(\frac{D}{m}\) με \(ω_ο^2\) έχουμε:
\[\frac{d^2x}{dt^2} + 2 \cdot Λ \cdot \frac{dx}{dt} + ω_ο^2 \cdot x = 0\]Για την καλύτερη κατανόηση των διαφορετικών περιπτώσεων (ισχυρή απόσβεση, κρίσιμη απόσβεση, ασθενής απόσβεση) και για χρήση μέσα στην σχολική αίθουσα δίνονται τα επόμενα κομμάτια κώδικα:
ισχυρή απόσβεση
DSolve[{x''[t] + 4 x'[t] + x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /. %, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ>ω_ο\) και το σχήμα
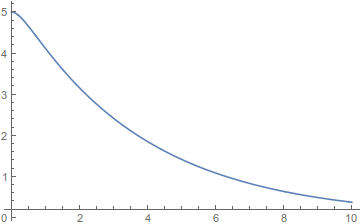
κρίσιμη απόσβεση
DSolve[{x''[t] + 2 x'[t] + x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /. %, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ=ω_ο\) και το σχήμα
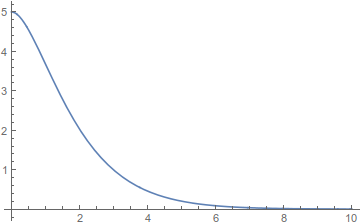
ασθενής απόσβεση (πρώτη περίπτωση)
DSolve[{x''[t] + 2 x'[t] + 4 x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /.%, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ<ω_ο\) και το σχήμα
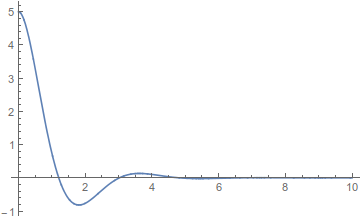
ασθενής απόσβεση (δεύτερη περίπτωση)
DSolve[{x''[t] + 2 x'[t] + 400 x[t] == 0, x[0] == 5, x'[0] == 0}, x[t], t]
Plot[x[t] /. %, {t, 0, 10}, PlotRange -> All]
δηλαδή \(Λ<ω_ο\) και το σχήμα
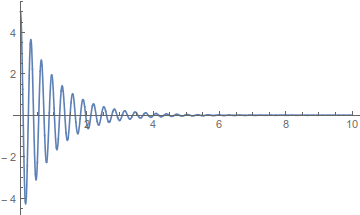
Ορισμοί για την Απλή Αρμονική Ταλάντωση
Ταλάντωση ονομάζεται μια περιοδική παλινδρομική κίνηση. Η ταλάντωση που γίνεται σε ευθεία τροχιά ονομάζεται γραμμική ταλάντωση. Απλή αρμονική ταλάντωση είναι μια ειδική περίπτωση γραμμικής ταλάντωσης σύμφωνα με την οποία ένα σώμα κινείται παλινδρομικά πάνω σε ένα άξονα γύρω από το σημείο Ο, που είναι μέσο της τροχιάς.
Περιοδικά φαινόμενα ονομάζονται τα φαινόμενα που εξελίσσονται και επαναλαμβάνονται αναλλοίωτα σε σταθερά χρονικά διαστήματα. Περίοδος ονομάζεται ο χρόνος που απαιτείται για να ολοκληρωθεί ένα περιοδικό φαινόμενο. Συχνότητα του περιοδικού φαινομένου ονομάζεται το πηλίκο του αριθμού των επαναλήψεων του φαινομένου προς τον αντίστοιχο χρόνο. Πλάτος της ταλάντωσης ονομάζεται η μέγιστη απομάκρυνση, δηλαδή η μέγιστη απόσταση από το σημείο Ο στην οποία φτάνει το κινητό.
Ορισμοί για την Φθίνουσα Ταλάντωση
Φθίνουσα ταλάντωση είναι μια ειδική περίπτωση γραμμικής ταλάντωσης σύμφωνα με την οποία ένα σώμα κινείται παλινδρομικά πάνω σε ένα άξονα γύρω από το σημείο Ο, που ονομάζεται σημείο αναφοράς. Στην φθίνουσα ταλάντωση η ενέργεια του κινητού συνεχώς μειώνεται.
Περίοδος ονομάζεται το χρονικό διάστημα μεταξύ δύο διαδοχικών διελεύσεων ενός κινητού από το σημείο Ο που ονομάζεται σημείο αναφοράς, με ταχύτητα ίδιας κατεύθυνσης. Συχνότητα ονομάζεται το πηλίκο του αριθμού των διελεύσεων του κινητού από το σημείο Ο, που ονομάζεται σημείο αναφοράς, με ταχύτητα ίδιας κατεύθυνσης.
blog comments powered by Disqus